第三章一元函数积分学及其应用

基础题

选择题

1 设$f(x)$是连续函数，且$f(x)\neq0$,若$\int xf(x)$d$x=\arcsin x+C$,则$\int\frac{\mathrm{d}x}{f(x)}=()$

A. $\frac13(1-x^2)^{\frac32}+C$
B. $\frac23(1-x^2)^{\frac32}+C$
C. $-\frac13(1-x^2)^{\frac32}+C$
D. $-\frac23(1-x^2)^{\frac32}+C$

第1步: 首先要知道$f(x)$的具体表达式,作为选择题应该如何快速计算呢?

利用积分与求导互为逆运算的性质
已知 $\int x f(x) \mathrm{d} x = \arcsin x + C$
对等式两边同时对 $x$ 求导
左边求导得到 $x f(x)$
右边求导得到 $\frac{1}{\sqrt{1-x^2}}$
因此，得到方程 $x f(x) = \frac{1}{\sqrt{1-x^2}}$
解这个方程，得到 $f(x) = \frac{1}{x \sqrt{1-x^2}}$
接下来，我们需要计算 $\int \frac{\mathrm{d}x}{f(x)}$
考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

第2步

首先排除分部法,因为分部法是针对被积函数中含有两种或以上不同类型函数相乘的题目.而这道题的被积函数只有一种类型
所以,初步判断应该使用换元法.对于含有根式的情况,可以使用第二类换元法,但这道题比较简单,也可以使用第一类换元法作整体代换,即凑积分的方法
令 $u = 1-x^2$，则 $\mathrm{d}u = -2x \mathrm{d}x$，即 $x \mathrm{d}x = -\frac{1}{2} \mathrm{d}u$
代入积分，得到 $\int x \sqrt{1-x^2} \mathrm{d}x = \int \sqrt{u} \cdot -\frac{1}{2} \mathrm{d}u = -\frac{1}{2} \int \sqrt{u} \mathrm{d}u$
计算 $\int \sqrt{u} \mathrm{d}u$，这是一个基本积分，结果是 $\frac{2}{3} u^{\frac{3}{2}}$
因此，$\int x \sqrt{1-x^2} \mathrm{d}x = -\frac{1}{2} \cdot \frac{2}{3} u^{\frac{3}{2}} = -\frac{1}{3} u^{\frac{3}{2}}$
代回 $u = 1-x^2$，得到 $\int x \sqrt{1-x^2} \mathrm{d}x = -\frac{1}{3} (1-x^2)^{\frac{3}{2}} + C$
所以选 C

2 设 $f(x)$ 是连续函数，$F(x)$ 是 $f(x)$ 的原函数，则( ).

A. 当 $f(x)$ 为奇函数时，$F(x)$ 必为偶函数
B. 当 $f(x)$ 为偶函数时，$F(x)$ 必为奇函数
C. 当 $f(x)$ 为周期函数时，$F(x)$ 必为周期函数
D. 当 $f(x)$ 为单调函数时，$F(x)$ 必为单调函数

第1步: 首先要明确奇函数和偶函数的定义是什么?

奇函数: $f(-x) = -f(x)$
偶函数: $f(-x) = f(x)$
原函数 $F(x)$ 是 $f(x)$ 的不定积分，即 $F(x) = \int f(x) \mathrm{d}x$
下面先使用定义,对选项A进行分析,寻找规律再分析其余选项,你能试试吗?

第2步

如果 $f(x)$ 是奇函数，即 $f(-x) = -f(x)$。
考虑 $F(x) = \int_a^x f(t) \mathrm{d}t$，我们需要验证 $F(-x)$ 是否等于 $F(x)$。
$F(-x) = \int_a^{-x} f(t) \mathrm{d}t$，通过变量替换 $u = -t$，得到 $F(-x) = \int_{-a}^x f(-u) \mathrm{d}u = \int_{-a}^x -f(u) \mathrm{d}u = -\int_{-a}^x f(u) \mathrm{d}u$。
由于 $f(x)$ 是奇函数，$\int_{-a}^x f(u) \mathrm{d}u$ 是一个奇函数的积分，结果是偶函数。
因此，$F(-x) = F(x)$，即 $F(x)$ 是偶函数。
作为单选题,已经可以确定选A.作为练习题,可以再检查一下其它选项,你能通过假设反例的方法快速验证一下吗?

第3步

选项 B: 当 $f(x)$ 为偶函数时，$F(x)$ 不一定为奇函数。例如，$f(x) = 1$ 是偶函数，但 $F(x) = x + C$ 不是奇函数。
选项 C: 当 $f(x)$ 为周期函数时，$F(x)$ 不一定为周期函数。例如，$f(x) = \tan(x)$ 是周期函数，但 $F(x) = -ln|\cos(x)| + C$ 不是周期函数。
选项 D: 当 $f(x)$ 为单调函数时，$F(x)$ 不一定为单调函数。例如，$f(x) = x$ 是单调函数，但 $F(x) = \frac{x^2}{2} + C$ 不是单调函数。
通过上述分析，只有选项 A 是正确的。

3 设 $F(x)$ 是 $\sin x^2$ 的一个原函数，则 $\mathrm{d}[ F( x^2) ] = ()$

A. $\sin x^4 \mathrm{d}x$
B. $\sin x^2 \mathrm{d}(x^2)$
C. $2x\sin x^2 \mathrm{d}x$
D. $2x\sin x^4 \mathrm{d}x$

第1步: 如何根据原函数的定义,把$F(x)$表示为具体的函数形式?

对于选择题,不一定要急于把原函数计算出来,可以先根据定义,表示出$F(x)$ 和 $\sin x^2$的关系
题目要求我们求 $\mathrm{d}[ F( x^2) ]$，其中 $F(x)$ 是 $\sin x^2$ 的一个原函数。
根据原函数的定义，$F(x)$ 满足 $F'(x) = \sin x^2$。
我们需要利用这个定义来求 $\mathrm{d}[ F( x^2) ]$。
接下来,显然应该使用链式求导法则来计算,具体应该如何做呢?

第2步

熟悉链式求导法则的同学可以跳过这一步,直接计算出结果.下面采用详细的代换步骤来进行说明
设 $u = x^2$，则 $F(x^2) = F(u)$。
根据链式法则，$\mathrm{d}[ F(u) ] = F'(u) \mathrm{d}u$。
由于 $u = x^2$，我们有 $\mathrm{d}u = 2x \mathrm{d}x$。
你能完成后续的计算吗?

第3步

代入 $u = x^2$ 和 $\mathrm{d}u = 2x \mathrm{d}x$，我们得到： $$ \mathrm{d}[ F( x^2) ] = F'(x^2) \mathrm{d}(x^2) = F'(x^2) \cdot 2x \mathrm{d}x $$
由于 $F'(x^2) = \sin (x^2)^2 = \sin x^4$，我们得到： $$ \mathrm{d}[ F( x^2) ] = \sin x^4 \cdot 2x \mathrm{d}x = 2x \sin x^4 \mathrm{d}x $$
通过上述推导，我们得出 $\mathrm{d}[ F( x^2) ] = 2x \sin x^4 \mathrm{d}x$。
因此，正确选项是 D。

4. 设 $f(x)=\begin{cases}\sin x,&0\leqslant x<\pi,\\2,&\pi\leqslant x\leqslant2\pi,\end{cases}F(x)=\int_{0}^{x}f(t)\mathrm{d}t$，则( ).

A. $x=\pi$ 是 $F(x)$ 的跳跃间断点
B. $x=\pi$ 是 $F(x)$ 的可去间断点
C. $F(x)$ 在 $x=\pi$ 处连续但不可导
D. $F(x)$ 在 $x=\pi$ 处可导

第1步: 首先分析 $f(x)$ 在定义域上的性质

$f(x)$ 在区间 $[0, \pi)$ 上是 $\sin x$，在区间 $[\pi, 2\pi]$ 上是常数 2。
观察 $f(x)$ 在 $x=\pi$ 处的行为：$f(x)$ 在 $x=\pi$ 处从 $\sin \pi = 0$ 跳跃到 2，这是一个跳跃间断点。
由于 $f(x)$ 在 $[0, 2\pi]$ 上只有有限个第一类间断点（即 $x=\pi$），根据知识点，$f(x)$ 在 $[0, 2\pi]$ 上是可积的。
接下来,你能分析 $F(x)$ 的性质吗?

第2步

由于 $f(x)$ 在 $[0, 2\pi]$ 上可积，根据知识点，$F(x) = \int_0^x f(t) \mathrm{d}t$ 在 $[0, 2\pi]$ 上是连续的。
特别地，$F(x)$ 在 $x=\pi$ 处连续。
再分析 $F(x)$ 在 $x=\pi$ 处的可导性是什么?

第3步

由于 $f(x)$ 在 $x=\pi$ 处不连续，根据知识点，$f(x)$ 在 $x=\pi$ 处没有原函数。
因此，$F(x)$ 在 $x=\pi$ 处不可导。
综上所述，$F(x)$ 在 $x=\pi$ 处连续但不可导。
因此，正确选项是 C。

注意:有以下知识点

设 $F(x)=\int_0^x f(t) \mathrm{d} t, x \in[a, b]$, 则
- $f(x)$ 在 $[a, b]$ 上可积 $\Rightarrow F(x)$ 在 $[a, b]$ 上连续;
- $f(x)$ 在 $[a, b]$ 上连续 $\Rightarrow F(x)$ 在 $[a, b]$ 上可导.
若 $f(x)$ 在 $[a, b]$ 上只有有限个第一类间断点, 则 $f(x)$ 在 $[a, b]$ 上可积.
若 $f(x)$ 在 $[a, b]$ 上存在第一类间断点, 则 $f(x)$ 没有原函数.

5. $f(x)=\begin{cases}x^2+1,&x\leqslant0,\\cos x,&x>0\end{cases}$的一个原函数为( )

A. $F(x)=\begin{cases}\frac{1}{3}x^3+x ,&x\leqslant0\\\\\sin x+1,&x>0\end{cases}$
B. $F(x)=\begin{cases}\frac{1}{3}x^3+x+1,&x\leqslant0\\\\\sin x+2,&x>0\end{cases}$
C. $F(x)=\begin{cases}\frac{1}{3}x^3+x+1,&x\leqslant0\\\\\sin x ,&x>0\end{cases}$
D. $F(x)=\begin{cases}\frac{1}{3}x^3+x ,&x\leqslant0\\\\\sin x ,&x>0\end{cases}$

第1步: 确定 $x \leqslant 0$ 时的原函数

当 $x \leqslant 0$ 时，$f(x) = x^2 + 1$
计算其不定积分：$F(x) = \int (x^2 + 1) \mathrm{d} x = \frac{1}{3} x^3 + x + C_1$
这里 $C_1$ 是积分常数
接下来,确定 $x > 0$ 时的原函数

第2步

当 $x > 0$ 时，$f(x) = \cos x$
计算其不定积分：$F(x) = \int \cos x \mathrm{d} x = \sin x + C_2$
这里 $C_2$ 是积分常数
下面如何确定常数项呢?

第3步

利用原函数的连续性确定常数
由于原函数 $F(x)$ 必须是连续的，因此在 $x = 0$ 处，左极限和右极限必须相等
计算左极限：$\lim_{x \to 0^-} F(x) = C_1$
计算右极限：$\lim_{x \to 0^+} F(x) = C_2$
因此，$C_1 = C_2$，令 $C_1 = C_2 = C$
确定最终的原函数形式是什么?

第4步

结合以上结果，原函数 $F(x)$ 可以表示为： $$ F(x) = \begin{cases} \frac{1}{3} x^3 + x + C, & x \leqslant 0\\ \sin x + C, & x > 0 \end{cases} $$
通过比较，选项 D 符合我们推导的形式，其中 $C = 0$

6. 设 $f(x)$ 在 $[0,1]$ 上连续，$f(x)>0, f^\prime(x)<0, f^{\prime\prime}(x)>0$，记 $M=\int_0^1f(x)\mathrm{d}x$，$N= f(1)$，$P= \frac{1}{2}[ f(0) + f(1) ]$，则 ( ).

A. $M< N< P$
B. $N< M< P$
C. $P< M< N$
D. $P< N< M$

第1步: 画出示意图,以理解题目条件和符号含义是什么?

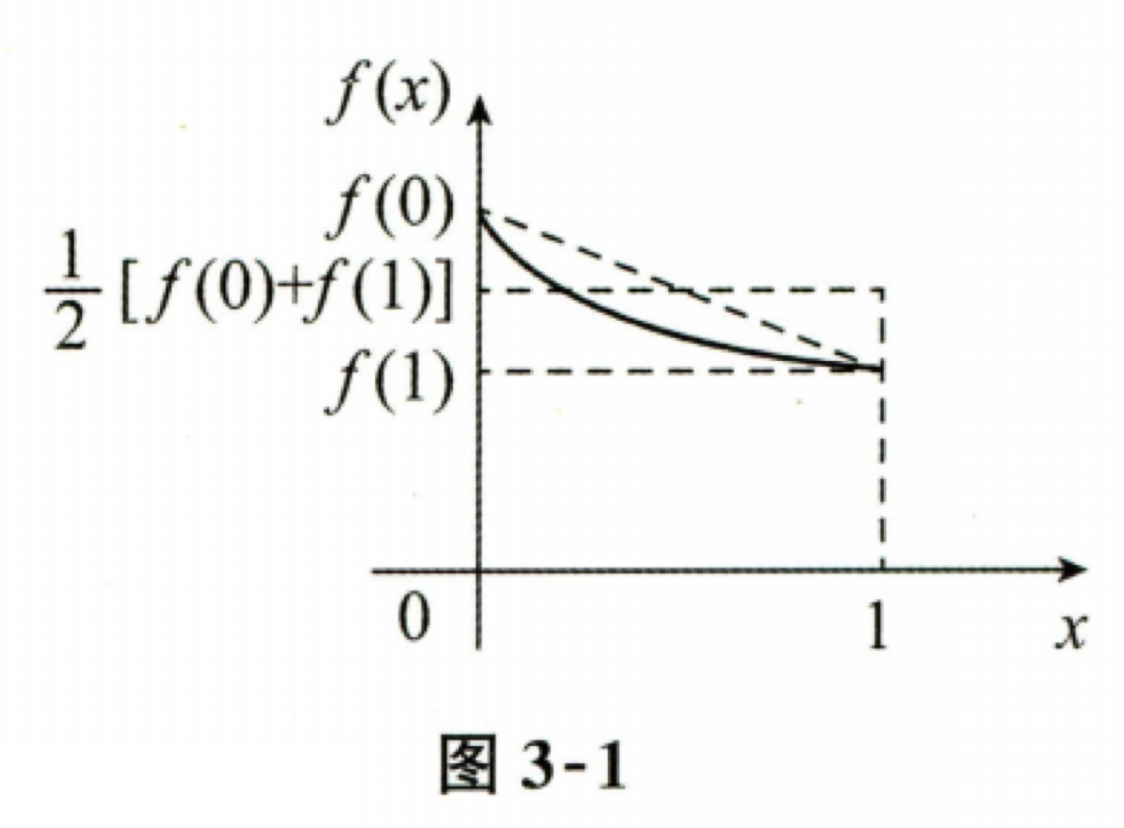
$f(x)$ 在 $[0,1]$ 上连续，且 $f(x)>0$，表示函数在区间 $[0,1]$ 上始终为正值。
$f^\prime(x)<0$，表示函数在区间 $[0,1]$ 上是单调递减的。
$f^{\prime\prime}(x)>0$，表示函数在区间 $[0,1]$ 上是凹函数。
$M=\int_0^1f(x)\mathrm{d}x$，表示函数 $f(x)$ 在区间 $[0,1]$ 上的定积分。
$N= f(1)$，表示函数在 $x=1$ 处的值。
$P= \frac{1}{2}[ f(0) + f(1) ]$，表示函数在 $x=0$ 和 $x=1$ 处的值的平均值。
接下来,你能分析各个值的大小关系吗?

第2步

由于 $f(x)$ 是单调递减的，$f(0) > f(1)$。
$M$ 是 $f(x)$ 在 $[0,1]$ 上的积分，由于 $f(x)$ 是单调递减的，$M$ 的值会小于 $f(0)$ 和 $f(1)$ 的平均值 $P$。
$N = f(1)$，由于 $f(x)$ 是单调递减的，$f(1)$ 是 $f(x)$ 在 $[0,1]$ 上的最小值，因此 $N < M$。
$P$ 是 $f(0)$ 和 $f(1)$ 的平均值，由于 $f(x)$ 是凹函数，$P$ 会大于 $M$。
通过上述分析，选项 B 是正确的，即 $N< M< P$。

7. 设 $\lim_{x\to0}\frac{1}{\sin x-ax}\int_b^x\frac{t^2}{\sqrt{1+t^2}}\mathrm{d}t=c$，且 $c\neq0$，则( ).

A. $a=1, b=0, c=-2$
B. $a=1, b=-2, c=-2$
C. $a=0, b=1, c=-2$
D. $a=1, b=1, c=1$

第1步: 对于求极限的题目,首先分析极限的分子和分母在 $x \to 0$ 时的行为

当 $x \to 0$ 时，$\sin x \approx x$，所以 $\sin x - ax \approx x - ax = (1 - a)x$。
如果 $a \neq 1$，则 $\sin x - ax$ 与 $x$ 是同阶无穷小。
观察积分 $\int_b^x \frac{t^2}{\sqrt{1+t^2}} \mathrm{d} t$，当 $x \to 0$ 时，积分也趋向于 0。
因此，如果 $a \neq 1$，分母 $\sin x - ax$ 与 $x$ 同阶，而分子 $\int_b^x \frac{t^2}{\sqrt{1+t^2}} \mathrm{d} t$ 是 $x$ 的高阶无穷小，极限结果为 0，与题设 $c \neq 0$ 矛盾。
所以，必须有 $a = 1$。
接下来,如何确定 $b$ 的值呢?

第2步

由于 $a = 1$，分母 $\sin x - x$ 在 $x \to 0$ 时趋向于 0。
为了使极限存在且 $c \neq 0$，积分 $\int_b^x \frac{t^2}{\sqrt{1+t^2}} \mathrm{d} t$ 也必须趋向于 0。
这意味着 $b$ 必须为 0，因为 $\int_0^x \frac{t^2}{\sqrt{1+t^2}} \mathrm{d} t$ 在 $x \to 0$ 时趋向于 0。
下面要求$c$,对一个积分式求极限，自然联想到洛必达法则，因为洛必达法则会对分子分母同时求导.你能计算一下试试吗?

第3步

现在我们有 $a = 1$ 和 $b = 0$，所以极限变为 $\lim_{x \to 0} \frac{1}{\sin x - x} \int_0^x \frac{t^2}{\sqrt{1+t^2}} \mathrm{d} t$。
使用洛必达法则，对分子和分母分别求导： $$ \lim_{x \to 0} \frac{\int_0^x \frac{t^2}{\sqrt{1+t^2}} \mathrm{d} t}{\sin x - x} = \lim_{x \to 0} \frac{\frac{x^2}{\sqrt{1+x^2}}}{\cos x - 1} $$
当 $x \to 0$ 时，$\cos x \approx 1 - \frac{x^2}{2}$，所以 $\cos x - 1 \approx -\frac{x^2}{2}$。
因此，极限变为： $$ \lim_{x \to 0} \frac{\frac{x^2}{\sqrt{1+x^2}}}{-\frac{x^2}{2}} = \lim_{x \to 0} -\frac{2x^2}{x^2 \sqrt{1+x^2}} = \lim_{x \to 0} -\frac{2}{\sqrt{1+x^2}} = -2 $$
综上所述，$a = 1$，$b = 0$，$c = -2$，所以正确答案是选项 A。

8. 下列反常积分收敛的是( ).

A. $\int_1^{+\infty}\frac{\mathrm{d}x}{x^2\sqrt{1+x}}$
B. $\int_0^1\frac{\mathrm{d}x}{\ln(1+x)}$
C. $\int_{-1}^1\frac{\mathrm{d}x}{\sin x}$
D. $\int_{-\infty}^{+\infty}\frac{x}{\sqrt{1+x^2}}\mathrm{d}x$

第1步: 判别反常积分敛散性的方法有哪些?

判别反常积分敛散性有两种方法:定义法和审敛法.
定义法，当积分计算较容易时，选择定义法判别.
反常积分的审敛法:
- 设 $I=\int_a^{+\infty} f(x) \mathrm{d} x, f(x)$ 非负连续, 则 $$ \lim_{x \rightarrow+\infty} x^\lambda f(x)=l, \begin{cases} 0 \leqslant l<+\infty \text { 且 } \lambda>1 \text {, 则收敛; } \\ 0<l \leqslant+\infty \text { 且 } \lambda \leqslant 1 \text {, 则发散. } \end{cases} $$
- 设 $I=\int_a^b f(x) \mathrm{d} x, x=a$ 是 $f(x)$ 的瑕点, $f(x)$ 非负连续, 则
两个常用结果: $$ \text { ( i ) } \int_1^{+\infty} \frac{\mathrm{d} x}{x^p}, \begin{cases} p>1 \text {, 收敛; } \\ p \leqslant 1 \text {, 发散. } \end{cases} \text { ( ii ) } \int_a^b \frac{\mathrm{d} x}{(x-a)^p}, \begin{cases} p<1 \text {, 收敛; } \\ p \geqslant 1 \text {, 发散. } \end{cases} $$
根据这些方法和结果, 我们可以逐一分析每个选项.

第2步: 分析选项 A

对于选项 A: $\int_1^{+\infty}\frac{\mathrm{d}x}{x^2\sqrt{1+x}}$
使用反常积分的审敛法: $$ \lim_{x \rightarrow+\infty} x^{\frac{5}{2}} \frac{1}{x^2 \sqrt{1+x}}=\lim_{x \rightarrow+\infty} \frac{1}{\sqrt{1+\frac{1}{x}}}=1 \left( \lambda=\frac{5}{2}>1,0<l=1<+\infty \right), $$
由于 $\lambda = \frac{5}{2} > 1$ 且 $0 < l = 1 < +\infty$, 故积分收敛.

第3步: 分析选项 B

对于选项 B: $\int_0^1\frac{\mathrm{d}x}{\ln(1+x)}$
$x=0$ 是 $\frac{1}{\ln (1+x)}$ 的瑕点. 使用反常积分的审敛法: $$ \lim_{x \rightarrow 0^{+}}(x-0) \frac{1}{\ln (1+x)}=1(\lambda=1,0<l<1<+\infty), $$
由于 $\lambda = 1$ 且 $0 < l < 1 < +\infty$, 知积分发散.

第4步: 分析选项 C

对于选项 C: $\int_{-1}^1\frac{\mathrm{d}x}{\sin x}$
$x=0$ 是 $\frac{1}{\sin x}$ 的瑕点. 使用反常积分的审敛法: $$ \lim_{x \rightarrow 0^{+}}(x-0) \frac{1}{\sin x}=1(\lambda=1,0<l=1<+\infty), $$
由于 $\lambda = 1$ 且 $0 < l = 1 < +\infty$, 知积分发散.

第5步: 分析选项 D

对于选项 D: $\int_{-\infty}^{+\infty}\frac{x}{\sqrt{1+x^2}}\mathrm{d}x$
使用定义法: $$ \int_{-\infty}^{+\infty} \frac{x}{\sqrt{1+x^2}} \mathrm{~d} x=\int_{-\infty}^1 \frac{x}{\sqrt{1+x^2}} \mathrm{~d} x+\int_1^{+\infty} \frac{x}{\sqrt{1+x^2}} \mathrm{~d} x $$
计算其中一个部分: $$ \lim_{a \rightarrow-\infty} \int_a^1 \frac{x \mathrm{~d} x}{\sqrt{1+x^2}}=\frac{1}{2} \lim_{a \rightarrow-\infty} \int_a^1 \frac{\mathrm{d}\left(1+x^2\right)}{\sqrt{1+x^2}}=\left.\frac{1}{2} \cdot 2 \lim_{a \rightarrow-\infty} \sqrt{1+x^2}\right|_a ^1=-\infty, $$
故积分发散.
综上可知, 选项 A 正确.

填空题

1 设 $F(x)$ 是 $f(x)$ 的一个原函数，$F\left(\frac{\pi}{4}\right) = 0$，当 $\frac{\pi}{4} < x < \frac{\pi}{2}$ 时，$F(x) > 0$，$F(x)f(x) = \frac{\ln(\tan x)}{\sin x \cos x}$，则 $f(x) = $

第1步: 如何利用原函数的定义替换条件式?

已知 $F(x)$ 是 $f(x)$ 的一个原函数，即 $F'(x) = f(x)$
将 $F'(x)$ 替换到条件式中，得到 $F(x)F'(x) = \frac{\ln(\tan x)}{\sin x \cos x}$
接下来应该如何处理这个等式?

第2步

观察到 $F(x)F'(x)$ 是一个乘积的形式，可以考虑将其两边同时积分
为了简化积分，可以先将等式两边乘以2，得到 $2F(x)F'(x) = \frac{2\ln(\tan x)}{\sin x \cos x}$
接下来对等式两边进行积分，得到 $$ \int 2F(x)F'(x) \mathrm{d}x = \int \frac{2\ln(\tan x)}{\sin x \cos x} \mathrm{d}x $$
左边的积分是一个常见的积分形式，可以直接得到 $F^2(x)$，即 $$ F^2(x) = \int \frac{2\ln(\tan x)}{\sin x \cos x} \mathrm{d}x $$
右边的积分观察发现,其中较复杂的部分 $\ln(\tan x)$ 的导数正好是 $[\ln(\tan x)]' = \frac{1}{\sin x \cos x}$
因此可以通过凑微分的方式处理，得到 $$ \int \frac{2\ln(\tan x)}{\sin x \cos x} \mathrm{d}x = [\ln(\tan x)]^2 + C $$
因此，得到 $F^2(x) = [\ln(\tan x)]^2 + C$
接下来应该如何确定常数 $C$?

第3步

已知 $F\left(\frac{\pi}{4}\right) = 0$，将其代入 $F^2(x) = [\ln(\tan x)]^2 + C$
当 $x = \frac{\pi}{4}$ 时，$\tan x = 1$，所以 $\ln(\tan x) = \ln 1 = 0$
代入得到 $0 = 0 + C$，所以 $C = 0$
因此，$F^2(x) = [\ln(\tan x)]^2$
如何求 $f(x)$?

第4步

由于 $F(x) > 0$，所以 $F(x) = \sqrt{[\ln(\tan x)]^2} = \ln(\tan x)$
因此，$f(x) = F'(x) = [\ln(\tan x)]'$
计算 $\ln(\tan x)$ 的导数，得到 $$ [\ln(\tan x)]' = \frac{1}{\tan x} \cdot \sec^2 x = \frac{\cos x}{\sin x} \cdot \frac{1}{\cos^2 x} = \frac{1}{\sin x \cos x} $$
所以，$f(x) = \frac{1}{\sin x \cos x}$

2 设对任意 $x$，有 $f(x+4) = f(x)$，且 $f'(x) = 1 + |x|$，$x \in [-2, 2]$，$f(0) = 1$，则 $f(9) = $

第1步: 利用周期性简化问题

题目给出 $f(x+4) = f(x)$，这意味着函数 $f(x)$ 是周期为 4 的周期函数。
因此，$f(9) = f(9 \mod 4) = f(1)$。这里的 $mod$ 就是求余数的意思,9除以4等于2,余数为1。
现在我们需要求 $f(1)$。
对于含有绝对值的函数应该如何处理呢?

第2步

题目给出 $f'(x) = 1 + |x|$，我们需要分段处理绝对值。
在区间 $[-2, 2]$ 内，$f'(x)$ 可以分为两段：
- 当 $-2 < x < 0$ 时，$f'(x) = 1 - x$。
- 当 $0 \leq x \leq 2$ 时，$f'(x) = 1 + x$。
对这两段分别积分：
- 对于 $-2 < x < 0$，积分 $f'(x) = 1 - x$： $$ f(x) = \int (1 - x) \, dx = x - \frac{x^2}{2} + C_1 $$
- 对于 $0 \leq x \leq 2$，积分 $f'(x) = 1 + x$： $$ f(x) = \int (1 + x) \, dx = x + \frac{x^2}{2} + C_2 $$
根据可导必连续,如何利用连续性确定常数项呢?

第3步

由于 $f(x)$ 在 $x = 0$ 处可导，因此 $f(x)$ 在 $x = 0$ 处连续。
这意味着 $f(0^-) = f(0) = f(0^+)$。
代入 $x = 0$：
- 从左边接近 $0$，$f(0^-) = 0 - \frac{0^2}{2} + C_1 = C_1$。
- 从右边接近 $0$，$f(0^+) = 0 + \frac{0^2}{2} + C_2 = C_2$。
由于 $f(0) = 1$，所以 $C_1 = C_2 = 1$。
接下来如何计算 $f(1)$ ?

第4步

现在我们知道 $f(x)$ 的具体表达式：
- 对于 $-2 < x < 0$，$f(x) = x - \frac{x^2}{2} + 1$。
- 对于 $0 \leq x \leq 2$，$f(x) = x + \frac{x^2}{2} + 1$。
计算 $f(1)$： $$ f(1) = 1 + \frac{1^2}{2} + 1 = 1 + \frac{1}{2} + 1 = \frac{5}{2} $$

3 设 $f(x) = \int_0^x \sin(x-t)^2 \mathrm{d}t$，则 $f'(x) = $

第1步: 对一个积分式求导,显然不需要真的求出积分.那么应该利用什么方式简化原式,直接得到答案呢?

题目要求求解函数 $f(x)$ 的导数 $f'(x)$。
$f(x)$ 是一个定积分，形式为 $\int_0^x \sin(x-t)^2 \mathrm{d}t$。
观察积分内部的函数 $\sin(x-t)^2$，可以考虑使用换元法来简化积分。
你觉得应该如何进行换元呢？

第2步

设 $u = x - t$，则 $du = -dt$。
当 $t = 0$ 时，$u = x$；当 $t = x$ 时，$u = 0$。
因此，积分可以变换为 $-\int_x^0 \sin u^2 \mathrm{d}u$。
由于积分限的改变，积分变为 $\int_0^x \sin u^2 \mathrm{d}u$。
这样，$f(x)$ 可以重新表示为 $f(x) = \int_0^x \sin u^2 \mathrm{d}u$。
接下来对积分式求导,可以直接去掉积分符号,具体应该怎样呢？

第3步

$\frac{d}{dx} \int_0^x g(u) \mathrm{d}u = g(x)$。
在这里，$g(u) = \sin u^2$，所以 $g(x) = \sin x^2$。
因此，$f'(x) = \sin x^2$。

4 设 $F(x) = \int_0^x t f(x^2 - t^2) \mathrm{d}t$，$f(x)$ 是连续函数，则 $F'(x) = $

第1步: 对一个积分式求导,显然不需要真的求出积分.那么应该利用什么方式简化原式,直接得到答案呢?

题目给出了一个积分函数 $F(x)$，要求我们求出 $F'(x)$
这里 $f(x)$ 是连续函数，注意 $t$ 是积分变量，$x$ 是积分上限
观察积分 $\int_0^x t f(x^2 - t^2) \mathrm{d}t$，我们可以尝试使用换元法来简化它
你觉得应该如何进行换元呢？

第2步

设 $u = x^2 - t^2$，那么 $\mathrm{d}u = -2t \mathrm{d}t$，即 $\mathrm{d}t = -\frac{1}{2t} \mathrm{d}u$
当 $t = 0$ 时，$u = x^2$；当 $t = x$ 时，$u = 0$
将这些代入原积分，得到 $$ \int_0^x t f(x^2 - t^2) \mathrm{d}t = \int_{x^2}^0 f(u) \left(-\frac{1}{2} \mathrm{d}u\right) = \frac{1}{2} \int_0^{x^2} f(u) \mathrm{d}u $$
这样我们就将原积分简化为了 $\frac{1}{2} \int_0^{x^2} f(u) \mathrm{d}u$
接下来应该如何求导呢?

第3步

现在我们需要对 $\frac{1}{2} \int_0^{x^2} f(u) \mathrm{d}u$ 求导
根据微积分基本定理，$\frac{\mathrm{d}}{\mathrm{d}x} \int_0^{x^2} f(u) \mathrm{d}u = f(x^2) \cdot \frac{\mathrm{d}}{\mathrm{d}x} (x^2)$
这里 $\frac{\mathrm{d}}{\mathrm{d}x} (x^2) = 2x$
因此，$F'(x) = \frac{1}{2} \cdot f(x^2) \cdot 2x = x f(x^2)$
这样我们就得到了 $F'(x)$ 的表达式

5 设 $F(x) = \int_0^x t f(x^2 - t^2) \mathrm{d}t$，$f(x)$ 在 $x=0$ 某邻域内可导，且 $f(0) = 0$，$f'(0) = 1$,则$\lim_{x\to0}\frac{F(x)}{x^4}= $

第1步: 对一个积分式求极限，自然联想到洛必达法则，因为洛必达法则会对分子分母同时求导.那么应该如何化简需要求解的式子呢?

由于积分和求导互为逆运算,所以可以化简
具体来说,对分子求导,得(这里利用了上一题的结论,即填空题第4题) $$ F'(x) = x f(x^2) $$
对分母求导,得 $$ (x^4)' = 4x^3 $$
因此,应用洛必达法则,得 $$ \lim_{x\to0}\frac{F(x)}{x^4} = \lim_{x\to0}\frac{F'(x)}{4x^3} = \lim_{x\to0}\frac{x f(x^2)}{4x^3} $$
接下来应该如何化简呢?

第2步

观察化简后的式子,发现分子分母都有$x$
因此可以约去$x$,得 $$ \lim_{x\to0}\frac{x f(x^2)}{4x^3} = \lim_{x\to0}\frac{f(x^2)}{4x^2} $$
注意,这时不能第二次使用洛必达法则,因为使用法则的前提是函数连续,题目只给出了 $f(x)$ 的连续性,由于没有 $f^{\prime}(x)$ 连续的条件,故 $\lim _{x \rightarrow 0} f^{\prime}(x)$ 未必存在.
接下来应该如何求极限呢?

第3步

观察化简后的式子,发现分子是一个函数,分母是一个多项式
因此可以尝试使用导数的定义,即 $$ \lim_{x\to0}\frac{f(x^2)}{4x^2} = \frac{1}{4} \lim_{x\to0}\frac{f(x^2)-f(0)}{x^2-0} $$
由于$f(0)=0$,且$f'(0)=1$,因此 $$ \frac{1}{4} \lim_{x\to0}\frac{f(x^2)-f(0)}{x^2-0} = \frac{1}{4} f'(0) = \frac{1}{4} $$

6 设 $\alpha(x) = \int_0^{5x} \frac{\sin t}{t} \mathrm{d}t$，$\beta(x) = \int_0^{\sin x} (1+t)^{\frac{1}{t}} \mathrm{d}t$，则 $\lim_{x \to 0} \frac{\alpha(x)}{\beta(x)} = $

第1步: 对一个积分式求极限，自然联想到洛必达法则，因为洛必达法则会对分子分母同时求导.那么应该如何化简需要求解的式子呢?

应用洛必达法则,对分子和分母同时求导
对于 $\alpha(x) = \int_0^{5x} \frac{\sin t}{t} \mathrm{d}t$, 根据积分和求导的互逆运算,可以直接写出积分结果
对于 $\beta(x) = \int_0^{\sin x} (1+t)^{\frac{1}{t}} \mathrm{d}t$, 同样根据积分和求导的互逆运算,可以直接写出积分结果
具体来说, $\alpha'(x) = \frac{\sin(5x)}{5x} \cdot 5 = 5 \cdot \frac{\sin(5x)}{5x}$
对于 $\beta'(x)$, 需要用到链式法则, $\beta'(x) = (1+\sin x)^{\frac{1}{\sin x}} \cdot \cos x$
接下来应该如何计算极限呢?

第2步

将求导后的结果代入极限表达式,得 $$ \lim_{x \to 0} \frac{\alpha(x)}{\beta(x)} = \lim_{x \to 0} \frac{5 \cdot \frac{\sin(5x)}{5x}}{(1+\sin x)^{\frac{1}{\sin x}} \cdot \cos x} $$
当 $x \to 0$ 时, $\sin(5x) \approx 5x$, 所以 $\frac{\sin(5x)}{5x} \to 1$
当 $x \to 0$ 时, $\sin x \to 0$, 所以 $(1+\sin x)^{\frac{1}{\sin x}} \to e$
当 $x \to 0$ 时, $\cos x \to 1$
因此,极限表达式化简为 $$ \lim_{x \to 0} \frac{5 \cdot 1}{e \cdot 1} = \frac{5}{e} $$
最终答案是 $\frac{5}{e}$

7 极限 $\lim_{x\to0}\frac{\int_{\cos x}^1t\ln t\mathrm{~d}t}{x^4}$=

第1步: 对一个积分式求极限，自然联想到洛必达法则，因为洛必达法则会对分子分母同时求导.那么应该如何化简需要求解的式子呢?

根据洛必达法则，我们需要对分子和分母分别求导。
分母的导数是 $4x^3$。
分子的导数是对定积分 $\int_{\cos x}^1 t \ln t \mathrm{~d}t$ 求导。
根据莱布尼茨定理，对定积分求导时，实际上只需对积分上限和下限分别求导。
即: $$ \frac{\mathrm{d}}{\mathrm{d}x} \left( \int_{a(x)}^{b(x)} f(t) \mathrm{d}t \right) = f(b(x)) \cdot \frac{\mathrm{d}b(x)}{\mathrm{d}x} - f(a(x)) \cdot \frac{\mathrm{d}a(x)}{\mathrm{d}x} $$
你能使用公式计算出这个导数吗？

第2步

根据莱布尼茨定理，$\frac{d}{dx} \int_1^{\cos x} t \ln t \mathrm{~d}t = \cos x \ln (\cos x) \cdot \frac{d}{dx} (\cos x) -0$。
其中, $\frac{d}{dx} (\cos x) = -\sin x$。
因此，$\frac{d}{dx} \int_1^{\cos x} t \ln t \mathrm{~d}t = \cos x \ln (\cos x) \cdot (-\sin x)$。
代入洛必达法则，得到 $\lim_{x \to 0} \frac{-\cos x \ln (\cos x) \cdot (-\sin x)}{4x^3}$。
你能简化这个表达式吗？

第3步

简化后得到 $\lim_{x \to 0} \frac{\cos x \ln (\cos x) \cdot \sin x}{4x^3}$。
由于 $\sin x \approx x$ 当 $x \to 0$，可以近似为 $\lim_{x \to 0} \frac{\cos x \ln (\cos x) \cdot x}{4x^3}$。
进一步简化得到 $\lim_{x \to 0} \frac{\cos x \ln (\cos x)}{4x^2}$。
由于 $\cos x \to 1$ 当 $x \to 0$，可以进一步简化。
你能继续应用洛必达法则吗？

第4步

对 $\frac{\cos x \ln (\cos x)}{4x^2}$ 再次应用洛必达法则。
分子和分母分别求导，得到 $\frac{-\sin x \ln (\cos x) + \cos x \cdot \frac{-\sin x}{\cos x}}{8x}$。
简化后得到 $\frac{-\sin x \ln (\cos x) - \sin x}{8x}$。
由于 $\sin x \approx x$ 当 $x \to 0$，可以近似为 $\frac{-x \ln (\cos x) - x}{8x}$。
进一步简化得到 $\frac{-\ln (\cos x) - 1}{8}$。
由于 $\ln (\cos x) \to 0$ 当 $x \to 0$，最终得到 $-\frac{1}{8}$。

8 极限 $\lim_{x\to 0}\frac{\int_0^x\left[\int_0^{u^2}\arctan(1+t)\mathrm{d}t\right]\mathrm{d}u}{x(1-cosx)}=$

第1步: 对一个积分式求极限，自然联想到洛必达法则，因为洛必达法则会对分子分母同时求导.那么应该如何化简需要求解的式子呢?

观察题目,分子是一个嵌套的积分,分母是一个简单的三角函数表达式
由于 $x \to 0$ 时,分母 $x(1-\cos x)$ 趋向于0,且分子也是一个积分,趋向于0
因此可以考虑使用洛必达法则,对分子和分母同时求导
首先,分母 $x(1-\cos x)$ 的导数是 $1 - \cos x + x \sin x$
注意,原书答案采用了等价无穷小替换,但实际上直接求导也可以算出正确答案,下面采取直接求导的方法处理
接下来,如何对分子进行求导呢?

第2步

分子 $\int_0^x\left[\int_0^{u^2}\arctan(1+t)\mathrm{d}t\right]\mathrm{d}u$ 是一个嵌套积分
根据莱布尼茨定理,对嵌套积分求导时,可以先对外层积分求导,再对内层积分求导
外层积分 $\int_0^x\left[\int_0^{u^2}\arctan(1+t)\mathrm{d}t\right]\mathrm{d}u$ 的导数是 $\int_0^{x^2}\arctan(1+t)\mathrm{d}t$
因此,分子求导后的结果是 $\int_0^{x^2}\arctan(1+t)\mathrm{d}t$
现在,分子和分母的导数分别是 $\int_0^{x^2}\arctan(1+t)\mathrm{d}t$ 和 $1 - \cos x + x \sin x$
接下来应该如何处理呢?

第3步

由于 $x \to 0$ 时,分母 $1 - \cos x + x \sin x$ 趋向于0,且分子 $\int_0^{x^2}\arctan(1+t)\mathrm{d}t$ 也趋向于0
因此可以再次使用洛必达法则,对分子和分母同时求导
分母 $1 - \cos x + x \sin x$ 的导数是 $\sin x + \sin x + x \cos x = 2 \sin x + x \cos x$
分子 $\int_0^{x^2}\arctan(1+t)\mathrm{d}t$ 的导数是 $2x \arctan(1+x^2)$
因此,分子和分母的导数分别是 $2x \arctan(1+x^2)$ 和 $2 \sin x + x \cos x$
接下来应该如何处理呢?

第4步

由于 $x \to 0$ 时,分母 $2 \sin x + x \cos x$ 趋向于0,且分子 $2x \arctan(1+x^2)$ 也趋向于0
因此可以再次使用洛必达法则,对分子和分母同时求导
分母 $2 \sin x + x \cos x$ 的导数是 $2 \cos x + \cos x - x \sin x = 3 \cos x - x \sin x$
分子 $2x \arctan(1+x^2)$ 的导数是 $2 \arctan(1+x^2) + 2x \cdot \frac{1}{1+(1+x^2)^2} \cdot 2x = 2 \arctan(1+x^2) + \frac{4x^2}{1+(1+x^2)^2}$
由于 $x \to 0$ 时, $\arctan(1+x^2) \to \arctan(1) = \frac{\pi}{4}$, 且 $\frac{4x^2}{1+(1+x^2)^2} \to 0$
因此,分子和分母的导数分别是 $2 \cdot \frac{\pi}{4} = \frac{\pi}{2}$ 和 $3 \cos 0 - 0 \cdot \sin 0 = 3$
最终,极限结果是 $\frac{\frac{\pi}{2}}{3} = \frac{\pi}{6}$

9 函数 $y=\frac{x^2}{\sqrt{1-x^2}}$ 在 $\left[\frac{1}{2},\frac{\sqrt{3}}{2}\right]$ 上的平均值为:

第1步: 求平均值需要求积分.在考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

观察被积函数 $\frac{x^2}{\sqrt{1-x^2}}$，发现含有 $\sqrt{1-x^2}$，这是一个典型的无理式，适合第二类换元法。
你觉得应该如何进行代换？

第2步

根据代换知识,应该使用三角代换
令 $x=\sin t$，则 $dx = \cos t \, dt$。
积分限也需要变换：当 $x=\frac{1}{2}$ 时，$t=\arcsin\left(\frac{1}{2}\right)=\frac{\pi}{6}$；当 $x=\frac{\sqrt{3}}{2}$ 时，$t=\arcsin\left(\frac{\sqrt{3}}{2}\right)=\frac{\pi}{3}$。
将这些代入原积分，得到 $$ \int_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}} \frac{x^2}{\sqrt{1-x^2}} \, dx = \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{\sin^2 t}{\cos t} \cos t \, dt = \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \sin^2 t \, dt $$
接下来应该如何处理 $\sin^2 t$？

第3步

使用三角恒等式 $\sin^2 t = \frac{1-\cos 2t}{2}$，将 $\sin^2 t$ 转换为更易积分的形式。
因此，积分变为 $$ \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \sin^2 t \, dt = \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{1-\cos 2t}{2} \, dt = \frac{1}{2} \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} (1-\cos 2t) \, dt $$
现在可以分别积分 $1$ 和 $\cos 2t$，你能完成这部分吗？

第4步

分别积分 $1$ 和 $\cos 2t$： $$ \frac{1}{2} \left[ \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} 1 \, dt - \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \cos 2t \, dt \right] $$
第一个积分 $\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} 1 \, dt = \frac{\pi}{3} - \frac{\pi}{6} = \frac{\pi}{6}$。
第二个积分 $\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \cos 2t \, dt$，令 $u=2t$，则 $du=2dt$，积分限变为 $\frac{\pi}{3}$ 到 $\frac{2\pi}{3}$，所以 $$ \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \cos 2t \, dt = \frac{1}{2} \int_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \cos u \, du = \frac{1}{2} [\sin u]_{\frac{\pi}{3}}^{\frac{2\pi}{3}} = \frac{1}{2} (\sin \frac{2\pi}{3} - \sin \frac{\pi}{3}) = \frac{1}{2} \left( -\frac{\sqrt{3}}{2} - \frac{\sqrt{3}}{2} \right) = -\frac{\sqrt{3}}{2} $$
因此，原积分的结果为 $$ \frac{1}{2} \left( \frac{\pi}{6} - (-\frac{\sqrt{3}}{2}) \right) = \frac{1}{2} \left( \frac{\pi}{6} + \frac{\sqrt{3}}{2} \right) = \frac{\pi}{12} $$
接下来平均值应该如何计算?

第5步

平均值的计算公式为 $\frac{1}{b-a} \int_a^b f(x)dx$，在这里 $a=\frac{1}{2}$，$b=\frac{\sqrt{3}}{2}$。
因此，平均值为 $$ \frac{\frac{\pi}{12}}{\frac{\sqrt{3}}{2} - \frac{1}{2}} = \frac{\frac{\pi}{12}}{\frac{\sqrt{3} - 1}{2}} = \frac{\pi}{12} \cdot \frac{2}{\sqrt{3} - 1} = \frac{\pi}{6} \cdot \frac{1}{\sqrt{3} - 1} = \frac{\pi (\sqrt{3} + 1)}{12} $$
最终答案是 $\frac{(\sqrt{3}+1) \pi}{12}$。

10 曲线 $y = \frac{\sqrt{x}}{1+x^2}$ 绕 $x$ 轴旋转一周所得的旋转体，将它在 $x=0$ 与 $x=\xi (\xi > 0)$ 之间部分的体积记为 $V(\xi)$，且 $V(a) = \frac{1}{2} \lim_{\xi \to +\infty} V(\xi)$，则 $a = $

第1步: 如何计算旋转体的体积?

旋转体的体积公式为 $V(\xi) = \pi \int_0^{\xi} y^2 \mathrm{~d} x$
其中 $y = \frac{\sqrt{x}}{1+x^2}$，所以 $y^2 = \frac{x}{(1+x^2)^2}$
因此，体积公式变为 $V(\xi) = \pi \int_0^{\xi} \frac{x}{(1+x^2)^2} \mathrm{~d} x$
你觉得应该如何计算这个积分呢?

第2步

这个积分可以通过换元法来计算
令 $u = 1 + x^2$，则 $\mathrm{d}u = 2x \mathrm{~d} x$，即 $\mathrm{d}x = \frac{\mathrm{d}u}{2x}$
当 $x = 0$ 时，$u = 1$；当 $x = \xi$ 时，$u = 1 + \xi^2$
因此，积分变为 $\int_1^{1+\xi^2} \frac{x}{u^2} \cdot \frac{\mathrm{d}u}{2x} = \frac{1}{2} \int_1^{1+\xi^2} \frac{1}{u^2} \mathrm{~d}u$
这个积分可以直接计算，得 $\frac{1}{2} \left[ -\frac{1}{u} \right]_1^{1+\xi^2} = \frac{1}{2} \left( -\frac{1}{1+\xi^2} + 1 \right)$
所以，$V(\xi) = \frac{\pi}{2} \left( 1 - \frac{1}{1+\xi^2} \right)$
如何求 $\lim_{\xi \to +\infty} V(\xi)$?

第3步

当 $\xi \to +\infty$ 时，$\frac{1}{1+\xi^2} \to 0$
因此，$\lim_{\xi \to +\infty} V(\xi) = \frac{\pi}{2}$
接下来,如何求 $a$?

第4步

根据题意，$V(a) = \frac{1}{2} \lim_{\xi \to +\infty} V(\xi)$
即 $\frac{\pi}{2} \left( 1 - \frac{1}{1+a^2} \right) = \frac{\pi}{4}$
解这个方程，得 $1 - \frac{1}{1+a^2} = \frac{1}{2}$
即 $\frac{1}{1+a^2} = \frac{1}{2}$
解得 $a^2 = 1$，即 $a = \pm 1$
由于 $a > 0$，所以 $a = 1$

11 曲线 $r = a \sin^3 \frac{\theta}{3} (a > 0, 0 \leqslant \theta \leqslant 3\pi)$ 的弧长 $s = $

第1步: 弧长公式是什么?

弧长公式为 $s = \int_0^{3\pi} \sqrt{r^2 + (r')^2} \, d\theta$
其中 $r = a \sin^3 \frac{\theta}{3}$，我们需要先求出 $r'$
计算 $r'$: $$ r' = \frac{d}{d\theta} \left( a \sin^3 \frac{\theta}{3} \right) = a \cdot 3 \sin^2 \frac{\theta}{3} \cdot \cos \frac{\theta}{3} \cdot \frac{1}{3} = a \sin^2 \frac{\theta}{3} \cos \frac{\theta}{3} $$
因此，$r' = a \sin^2 \frac{\theta}{3} \cos \frac{\theta}{3}$
下面代入弧长公式,应该如何计算?

第2步

代入 $r$ 和 $r'$ 到弧长公式中: $$ s = \int_0^{3\pi} \sqrt{a^2 \sin^6 \frac{\theta}{3} + a^2 \sin^4 \frac{\theta}{3} \cos^2 \frac{\theta}{3}} \, d\theta $$
提取公因子 $a^2 \sin^4 \frac{\theta}{3}$: $$ s = a \int_0^{3\pi} \sin^2 \frac{\theta}{3} \sqrt{\sin^2 \frac{\theta}{3} + \cos^2 \frac{\theta}{3}} \, d\theta $$
由于 $\sin^2 x + \cos^2 x = 1$，所以: $$ s = a \int_0^{3\pi} \sin^2 \frac{\theta}{3} \, d\theta $$
这个积分应该如何计算呢?

第3步

可以使用换元法简化积分
令 $t = \frac{\theta}{3}$，则 $d\theta = 3 \, dt$，积分限变为 $0$ 到 $\pi$: $$ s = 3a \int_0^\pi \sin^2 t \, dt $$
使用半角公式 $\sin^2 t = \frac{1 - \cos 2t}{2}$: $$ s = 3a \int_0^\pi \frac{1 - \cos 2t}{2} \, dt = \frac{3a}{2} \int_0^\pi (1 - \cos 2t) \, dt $$
你能完成剩下的积分运算吗?

第4步

分别计算两个积分: $$ \int_0^\pi 1 \, dt = \pi $$ $$ \int_0^\pi \cos 2t \, dt = \left[ \frac{\sin 2t}{2} \right]_0^\pi = 0 $$
因此: $$ s = \frac{3a}{2} (\pi - 0) = \frac{3\pi a}{2} $$

12 曲线 $y = \int_{-\frac{\pi}{2}}^x \sqrt{\cos t} \mathrm{d}t$ 的全长 $s = $

第1步: 由这个积分式所定义的函数,它的定义域不等同于积分的上下限,所以首先要明确这个函数自身的定义域,应该是什么呢?

$\sqrt{\cos t}$ 要有意义,且应该在积分上下限之内
因此，函数 $y = \int_{-\frac{\pi}{2}}^x \sqrt{\cos t} \mathrm{d}t$ 的定义域为 $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$。
接下来应该把曲线的弧长用条件表示出来,应该如何表示呢?

第2步

曲线的全长 $s$ 可以通过积分 $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sqrt{1 + y'^2} \mathrm{d}x$ 来计算。
代入 $y' = \sqrt{\cos x}$，我们得到 $$ s = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sqrt{1 + (\sqrt{\cos x})^2} \mathrm{d}x = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sqrt{1 + \cos x} \mathrm{d}x. $$
对于含有三角函数,同时又是根式的函数,这个积分应该如何计算呢?

第4步

注意到 $\sqrt{1 + \cos x}$ 可以进一步简化。利用半角公式 $1 + \cos x = 2 \cos^2 \frac{x}{2}$，我们得到 $$ \sqrt{1 + \cos x} = \sqrt{2 \cos^2 \frac{x}{2}} = \sqrt{2} \cos \frac{x}{2}. $$
因此，积分变为 $$ s = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sqrt{2} \cos \frac{x}{2} \mathrm{d}x. $$
接下来的部分应该如何计算?

第5步

由于 $\sqrt{2}$ 是常数，可以提到积分号外面，得到 $$ s = \sqrt{2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos \frac{x}{2} \mathrm{d}x. $$
计算 $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos \frac{x}{2} \mathrm{d}x$，令 $u = \frac{x}{2}$，则 $\mathrm{d}u = \frac{1}{2} \mathrm{d}x$，积分限变为 $-\frac{\pi}{4}$ 和 $\frac{\pi}{4}$，因此 $$ \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos \frac{x}{2} \mathrm{d}x = 2 \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \cos u \mathrm{d}u = 2 \left[ \sin u \right]_{-\frac{\pi}{4}}^{\frac{\pi}{4}} = 2 (\sin \frac{\pi}{4} - \sin -\frac{\pi}{4}) = 2 \cdot \sqrt{2} = 2\sqrt{2}. $$
因此，$s = \sqrt{2} \cdot 2\sqrt{2} = 4$。

13 由曲线 $y = \ln x$ 与两直线 $y = (e+1)-x$ 及 $y=0$ 所围平面图形的面积 $S =$

第1步: 先把围成的图形绘制出来,确定各个交点.

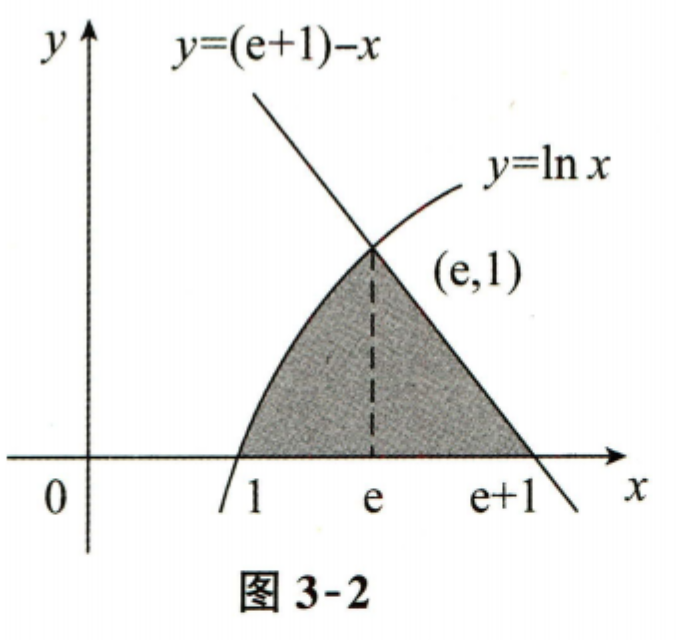
首先，我们需要确定曲线 $y = \ln x$ 与直线 $y = (e+1)-x$ 及 $y=0$ 的交点。
曲线 $y = \ln x$ 与 $y=0$ 的交点是 $x=1$。
直线 $y = (e+1)-x$ 与 $y=0$ 的交点是 $x=e+1$。
曲线 $y = \ln x$ 与直线 $y = (e+1)-x$ 的交点可以通过解方程 $\ln x = (e+1)-x$ 来确定。设交点为 $x=a$，则 $\ln a = (e+1)-a$。
通过观察和计算，可以发现 $a=e$。
因此，积分区域由 $x=1$ 到 $x=e+1$。
选择 $y$ 作为积分变量会更简单，因为 $y$ 的范围是从 $0$ 到 $\ln e = 1$。
接下来,把面积用积分表示出来,应该是什么呢?

第2步

使用 $y$ 作为积分变量，$y$ 的范围是从 $0$ 到 $1$。
在 $y$ 的范围 $[0, 1]$ 内，曲线 $y = \ln x$ 对应的 $x$ 值为 $x = e^y$。
直线 $y = (e+1)-x$ 对应的 $x$ 值为 $x = (e+1)-y$。
因此，面积 $S$ 可以表示为： $$ S = \int_0^1 \left[ ((e+1)-y) - e^y \right] \mathrm{d} y $$
这个积分应该如何计算?

第3步

现在我们计算上述积分： $$ S = \int_0^1 \left[ (e+1)-y - e^y \right] \mathrm{d} y $$
这个积分可以拆分为三个部分： $$ S = \int_0^1 (e+1) \mathrm{d} y - \int_0^1 y \mathrm{d} y - \int_0^1 e^y \mathrm{d} y $$
分别计算每个部分： $$ \int_0^1 (e+1) \mathrm{d} y = (e+1) \cdot 1 = e+1 $$ $$ \int_0^1 y \mathrm{d} y = \left[ \frac{y^2}{2} \right]_0^1 = \frac{1}{2} $$ $$ \int_0^1 e^y \mathrm{d} y = \left[ e^y \right]_0^1 = e - 1 $$
将这些结果代入原积分： $$ S = (e+1) - \frac{1}{2} - (e-1) = e + 1 - \frac{1}{2} - e + 1 = 2 - \frac{1}{2} = \frac{3}{2} $$

14 设 $D$ 是由曲线 $y = \sin x + 1$ 与直线 $x=0$，$x=\pi$，$y=0$ 所围平面图形，则 $D$ 绕 $x$轴旋转一周所得旋转体的体积$V= $

第1步: 旋转体体积的计算公式是什么?

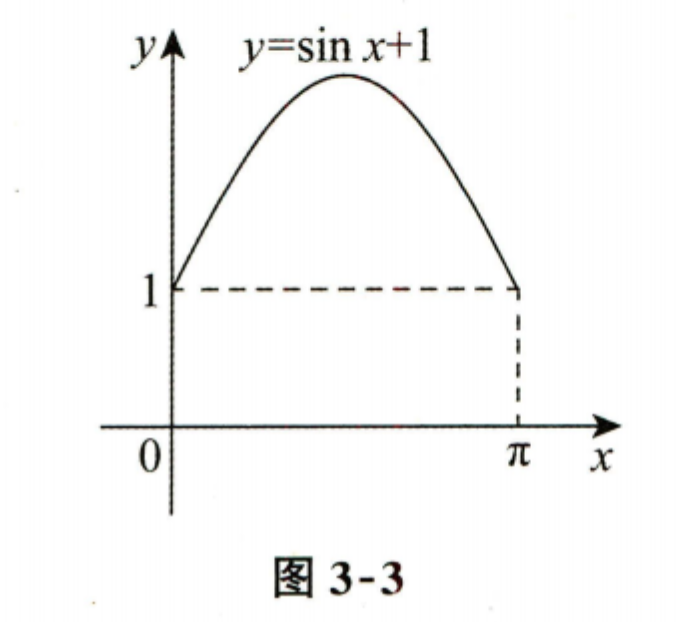
根据旋转体体积的计算公式，绕 $x$ 轴旋转一周的体积 $V$ 可以表示为： $$ V = \int_0^\pi \pi y^2 \mathrm{d} x $$
其中 $y = \sin x + 1$，因此体积公式变为： $$ V = \int_0^\pi \pi (\sin x + 1)^2 \mathrm{d} x $$
你能展开 $(\sin x + 1)^2$ 并进行积分吗？

第2步

首先展开 $(\sin x + 1)^2$： $$ (\sin x + 1)^2 = \sin^2 x + 2 \sin x + 1 $$
利用三角恒等式 $\sin^2 x = \frac{1 - \cos 2x}{2}$，我们可以进一步简化： $$ \sin^2 x + 2 \sin x + 1 = \frac{1 - \cos 2x}{2} + 2 \sin x + 1 $$
合并常数项： $$ \frac{1 - \cos 2x}{2} + 2 \sin x + 1 = \frac{3}{2} + 2 \sin x - \frac{\cos 2x}{2} $$
因此，体积公式变为： $$ V = \pi \int_0^\pi \left( \frac{3}{2} + 2 \sin x - \frac{\cos 2x}{2} \right) \mathrm{d} x $$
你能分别计算这些积分吗？

第3步

分别计算每一部分的积分： $$ \int_0^\pi \frac{3}{2} \mathrm{d} x = \frac{3}{2} \pi $$ $$ \int_0^\pi 2 \sin x \mathrm{d} x = 2 \left[ -\cos x \right]_0^\pi = 2 (1 - (-1)) = 4 $$ $$ \int_0^\pi -\frac{\cos 2x}{2} \mathrm{d} x = -\frac{1}{2} \left[ \frac{\sin 2x}{2} \right]_0^\pi = 0 $$
将这些结果相加： $$ V = \pi \left( \frac{3}{2} \pi + 4 + 0 \right) = \frac{3}{2} \pi^2 + 4 \pi $$

15 设 $n$ 为正数，$\lim_{x \to 0} \left( \frac{n-x}{n+x} \right)^{\frac{2}{x}} = \int_{\frac{1}{n}}^{+\infty} x \mathrm{e}^{-4x} \mathrm{d}x$，则 $n = $

第1步: 计算极限 $\lim_{x \to 0} \left( \frac{n-x}{n+x} \right)^{\frac{2}{x}}$

首先，我们需要处理极限的形式。注意到 $\left( \frac{n-x}{n+x} \right)$ 在 $x \to 0$ 时趋近于 1。
使用指数和对数变换，我们可以将极限转换为更易处理的形式： $$ \lim_{x \to 0} \left( \frac{n-x}{n+x} \right)^{\frac{2}{x}} = \lim_{x \to 0} \exp\left( \frac{2}{x} \ln \left( \frac{n-x}{n+x} \right) \right) $$
由于 $\ln \left( \frac{n-x}{n+x} \right)$ 在 $x \to 0$ 时趋近于 0，我们可以使用泰勒展开 $\ln(1+y) \approx y$ 当 $y \to 0$： $$ \ln \left( \frac{n-x}{n+x} \right) \approx \ln \left( 1 - \frac{2x}{n+x} \right) \approx -\frac{2x}{n+x} $$
因此，极限变为： $$ \lim_{x \to 0} \exp\left( \frac{2}{x} \cdot -\frac{2x}{n+x} \right) = \exp\left( -\frac{4}{n+x} \right) $$
当 $x \to 0$，这进一步简化为： $$ \exp\left( -\frac{4}{n} \right) $$
接下来如何计算积分呢?这个积分适用什么积分方法呢?

第2步

这个积分含有两种不同类型的函数相乘,属于典型的适用分部法的积分.
根据口诀使用分部积分法，设 $u = x$ 和 $dv = \mathrm{e}^{-4x} \mathrm{d}x$，则 $du = \mathrm{d}x$ 和 $v = -\frac{1}{4} \mathrm{e}^{-4x}$： $$ \int_{\frac{1}{n}}^{+\infty} x \mathrm{e}^{-4x} \mathrm{d}x = \left. -\frac{1}{4} x \mathrm{e}^{-4x} \right|{\frac{1}{n}}^{+\infty} + \frac{1}{4} \intx $$}{n}}^{+\infty} \mathrm{e}^{-4x} \mathrm{d
计算边界值： $$ \left. -\frac{1}{4} x \mathrm{e}^{-4x} \right|_{\frac{1}{n}}^{+\infty} = 0 - \left( -\frac{1}{4 n} \mathrm{e}^{-\frac{4}{n}} \right) = \frac{1}{4 n} \mathrm{e}^{-\frac{4}{n}} $$
继续计算第二个积分： $$ \frac{1}{4} \int_{\frac{1}{n}}^{+\infty} \mathrm{e}^{-4x} \mathrm{d}x = \frac{1}{4} \left. -\frac{1}{4} \mathrm{e}^{-4x} \right|_{\frac{1}{n}}^{+\infty} = \frac{1}{4} \cdot \frac{1}{4} \mathrm{e}^{-\frac{4}{n}} = \frac{1}{16} \mathrm{e}^{-\frac{4}{n}} $$
因此，积分结果为： $$ \int_{\frac{1}{n}}^{+\infty} x \mathrm{e}^{-4x} \mathrm{d}x = \frac{1}{4 n} \mathrm{e}^{-\frac{4}{n}} + \frac{1}{16} \mathrm{e}^{-\frac{4}{n}} $$
结合极限和积分结果求解 $n$,你能完成后面的部分吗?

第3步

根据题设，极限和积分结果相等： $$ \exp\left( -\frac{4}{n} \right) = \frac{1}{4 n} \mathrm{e}^{-\frac{4}{n}} + \frac{1}{16} \mathrm{e}^{-\frac{4}{n}} $$
将 $\mathrm{e}^{-\frac{4}{n}}$ 提到等式左边： $$ \mathrm{e}^{-\frac{4}{n}} = \left( \frac{1}{4 n} + \frac{1}{16} \right) \mathrm{e}^{-\frac{4}{n}} $$
消去 $\mathrm{e}^{-\frac{4}{n}}$： $$ 1 = \frac{1}{4 n} + \frac{1}{16} $$
解这个方程： $$ 1 = \frac{4 + n}{16 n} \implies 16 n = 4 + n \implies 15 n = 4 \implies n = \frac{4}{15} $$

16 计算细棒的质心坐标 $\overline{x}=$

第1步: 理解质心坐标的定义和公式

质心坐标的定义是：对于一个在区间 $[a, b]$ 上的细棒，其质心坐标 $\overline{x}$ 可以通过以下公式计算： $$ \overline{x} = \frac{\int_a^b x \rho(x) \mathrm{d} x}{\int_a^b \rho(x) \mathrm{d} x} $$
其中，$\rho(x)$ 是细棒在 $x$ 处的线密度。
在本题中，区间是 $[0, 1]$，线密度 $\rho(x) = 2x + 1$。
你能根据这个公式写出具体的积分表达式吗？

第2步

根据公式，分子部分的积分是 $\int_0^1 x \rho(x) \mathrm{d} x$。
代入 $\rho(x) = 2x + 1$，得到： $$ \int_0^1 x (2x + 1) \mathrm{d} x = \int_0^1 (2x^2 + x) \mathrm{d} x $$
这个积分可以拆分成两个基本积分： $$ \int_0^1 2x^2 \mathrm{d} x + \int_0^1 x \mathrm{d} x $$
你能分别计算这两个积分吗？

第3步

根据公式，分母部分的积分是 $\int_0^1 \rho(x) \mathrm{d} x$。
代入 $\rho(x) = 2x + 1$，得到： $$ \int_0^1 (2x + 1) \mathrm{d} x $$
这个积分也可以拆分成两个基本积分： $$ \int_0^1 2x \mathrm{d} x + \int_0^1 1 \mathrm{d} x $$
你能分别计算这两个积分吗？

第4步

对于分子部分的积分： $$ \int_0^1 2x^2 \mathrm{d} x = 2 \int_0^1 x^2 \mathrm{d} x = 2 \left[ \frac{x^3}{3} \right]_0^1 = 2 \cdot \frac{1}{3} = \frac{2}{3} $$ $$ \int_0^1 x \mathrm{d} x = \left[ \frac{x^2}{2} \right]_0^1 = \frac{1}{2} $$
因此，分子部分的积分值为： $$ \int_0^1 (2x^2 + x) \mathrm{d} x = \frac{2}{3} + \frac{1}{2} = \frac{4}{6} + \frac{3}{6} = \frac{7}{6} $$
对于分母部分的积分： $$ \int_0^1 2x \mathrm{d} x = 2 \int_0^1 x \mathrm{d} x = 2 \left[ \frac{x^2}{2} \right]_0^1 = 2 \cdot \frac{1}{2} = 1 $$ $$ \int_0^1 1 \mathrm{d} x = \left[ x \right]_0^1 = 1 $$
因此，分母部分的积分值为： $$ \int_0^1 (2x + 1) \mathrm{d} x = 1 + 1 = 2 $$
最后,如何计算质心坐标 $\overline{x}$?

第5步

根据质心坐标的公式，质心坐标 $\overline{x}$ 为： $$ \overline{x} = \frac{\int_0^1 x \rho(x) \mathrm{d} x}{\int_0^1 \rho(x) \mathrm{d} x} = \frac{\frac{7}{6}}{2} = \frac{7}{12} $$
因此，细棒的质心坐标 $\overline{x}$ 为 $\frac{7}{12}$。

17 $\lim_{n\to\infty}\sum_{k=1}^n\frac1n\mathrm{ln}\frac{n+2k}{3n-2k}=$

第1步: 这道题是一个求和的极限问题，涉及到积分的定义。我们需要将求和转换为积分形式.应该如何转化呢?

观察求和的形式，可以发现它类似于定积分的定义形式 $\lim_{n\to\infty}\sum_{k=1}^n f\left(\frac{k}{n}\right)\frac{1}{n}$，其中 $f(x)$ 是某个函数。
观察求和项 $\frac{1}{n} \ln \frac{n+2k}{3n-2k}$，可以将其改写为 $\frac{1}{n} \ln \left(1 + \frac{2k}{n}\right) - \frac{1}{n} \ln \left(3 - \frac{2k}{n}\right)$。
这表明我们可以将其视为对函数 $\ln \left(1 + \frac{2k}{n}\right) - \ln \left(3 - \frac{2k}{n}\right)$ 的积分。
具体来说，我们可以将其转换为积分形式： $$ \lim_{n\to\infty}\sum_{k=1}^n \frac{1}{n} \ln \frac{n+2k}{3n-2k} = \lim_{n\to\infty} \frac{1}{2} \sum_{k=1}^n \frac{2-0}{n} \ln \frac{1+\frac{2k}{n}}{3-\frac{2k}{n}} $$
这可以进一步简化为： $$ \frac{1}{2} \int_0^2 \ln \frac{1+x}{3-x} \mathrm{~d} x $$
如何求解这个积分呢?

第2步

为了进一步简化积分，我们可以使用换元法。令 $x = 1 + t$，则 $dx = dt$，积分限从 $0$ 到 $2$ 变为 $-1$ 到 $1$。
因此，积分变为： $$ \frac{1}{2} \int_{-1}^1 \ln \frac{2+t}{2-t} \mathrm{~d} t $$

第3步

观察被积函数 $\ln \frac{2+t}{2-t}$，可以发现它是一个奇函数，因为 $\ln \frac{2+t}{2-t} = -\ln \frac{2-t}{2+t}$。
奇函数在一个对称区间上的积分为零，因此： $$ \frac{1}{2} \int_{-1}^1 \ln \frac{2+t}{2-t} \mathrm{~d} t = 0 $$
如果没有观察到奇偶性,也可以直接进行积分运算.利用对数函数的性质,把被积函数拆开成两项,即 $\frac{1}{2} \int_0^2 \ln \frac{1+x}{3-x} \mathrm{~d} x=\frac{1}{2}\left[\int_0^2 \ln (1+x) \mathrm{d} x-\int_0^2 \ln (3-x) \mathrm{d} x\right]$, 利用分部积分法分别计算两个积分亦可.
不过后一种方法计算量大,比较慢.在选择题中对于定积分,应当优先考虑奇偶性.

解答题

1.求积分

1.1 $\int\frac{2^x \cdot 3^x}{9^x-4^x}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先排除分部法,因为分部法是针对被积函数中含有两种或以上不同类型函数相乘的题目.而这道题的被积函数全都属于指数函数,即只有一种类型的函数
再排除第二类换元法,因为它是针对整体无法拆分成几个部分的无理式.这道题不含无理式
因此初步判断,此题属于恒等变形+第一类换元法
你觉得应该如何变形,来寻找换元的部分呢?

第2步

观察题目发现分母中9和4正好是3和2的平方
因此先尝试把它们写成平方的形式,即 $I=\int\frac{2^x \cdot 3^x}{(3^x)^2-(4^x)^2}\mathrm{d}x$
为了把两个含有x的量整合到一起,可以分子分母同时除以$(2^x)^2$,即 $\int\frac{2^x \cdot 3^x}{(3^x)^2-(4^x)^2}\mathrm{d}x=\int\frac{\frac{3^x}{2^x}}{(\frac{3^x}{2^x})^2-1}\mathrm{d}x$
现在可以令 $u=\frac{3^x}{2^x}$
接下来应该如何代换呢?

第3步

$u=\frac{3^x}{2^x} = (\frac{3}{2})^x$,故 $x=log_\frac{3}{2}u$
所以 $dx=\frac{1}{uln\frac{3}{2}}\mathrm{d}u$
将换元代入原式并作化简,其中常数可以提到积分外面,得 $$ I=\int\frac{\cancel{u}}{u^2-1} \cdot \frac{1}{\cancel{u}ln\frac{3}{2}}\mathrm{d}u = \frac{1}{ln\frac{3}{2}}\int\frac{1}{u^2-1}\mathrm{d}u $$
剩下的积分应该如何计算呢?

第4步

$\int\frac{1}{u^2-1}\mathrm{d}u$ 不属于基本积分表要求记忆的公式,但它属于考试常见公式
如果你不记得这个公式,那么可以使用下列步骤来求解:
其中被积函数可以拆开成两个式子的差,即 $\frac{1}{u^2-1}=\frac{1}{2}(\frac{1}{u-1}-\frac{1}{u+1})$
因此 $$ \frac{1}{ln\frac{3}{2}}\int\frac{1}{u^2-1}\mathrm{d}u = \frac{1}{ln\frac{3}{2}}\cdot \frac{1}{2}(\int\frac{1}{u-1}\mathrm{d}u - \int\frac{1}{u+1}\mathrm{d}u) $$
现在可以直接积分,得 $$ I=\frac{1}{2ln\frac{3}{2}}(ln|u-1| - ln|u+1|)+C $$
最后要把换元的部分代回原式,你能完成剩余的部分吗?

第5步

换元代回原式并整理,得 $$ I=\frac{1}{2ln\frac{3}{2}}(ln|3^x-2^x| - ln|3^x+2^x|)+C = \frac{1}{2ln\frac{3}{2}}ln\left|\frac{3^x-2^x}{3^x+2^x}\right|+C $$

1.2 $\int \frac{\mathrm{d}x}{x^2(1 - x^4)}$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先排除分部法,因为分部法是针对被积函数中,含有两种或以上不同类型函数相乘的题目.而这道题的被积函数只含有幂函数,即只有一种类型的函数
再排除第二类换元法,因为它是针对整体无法拆分成几个部分的无理式.这道题不含无理式
因此初步判断,此题属于恒等变形+第一类换元法
你觉得应该如何变形,来寻找换元的部分呢?

第2步

观察题目发现分母中有一个$x^2$和一个$x^4$
为了方便裂项,我们可以先将分母中的$x^2$变为$x^4$,即 $\int \frac{\mathrm{d}x}{x^2(1 - x^4)} = \int \frac{x^2}{x^4(1 - x^4)} \mathrm{d}x$
这样分子也多了一个$x^2$,我们可以将其提出来,即 $\int x^2 \left( \frac{1}{x^4} + \frac{1}{1 - x^4} \right) \mathrm{d}x$
接下来应该如何裂项呢?

第3步

将积分拆分成两个部分,即 $\int \frac{1}{x^2} \mathrm{d}x + \int \frac{1 + x^2 - 1}{1 - x^4} \mathrm{d}x$
第一个积分 $\int \frac{1}{x^2} \mathrm{d}x$ 可以直接套用公式,得到 $-\frac{1}{x}$
第二个积分 $\int \frac{1 + x^2 - 1}{1 - x^4} \mathrm{d}x$ 需要进一步裂项,即 $\int \frac{\mathrm{d}x}{1 - x^2} - \int \frac{\mathrm{d}x}{1 - x^4}$
接下来应该如何处理这两个积分呢?

第4步

对于 $\int \frac{\mathrm{d}x}{1 - x^2}$,我们可以使用裂项法,即 $\frac{1}{1 - x^2} = \frac{1}{2} \left( \frac{1}{1 - x} + \frac{1}{1 + x} \right)$
因此 $\int \frac{\mathrm{d}x}{1 - x^2} = \frac{1}{2} \int \frac{1}{1 - x} \mathrm{d}x + \frac{1}{2} \int \frac{1}{1 + x} \mathrm{d}x = \frac{1}{2} \ln \left| \frac{1 + x}{1 - x} \right|$
对于 $\int \frac{\mathrm{d}x}{1 - x^4}$,我们可以使用裂项法,即 $\frac{1}{1 - x^4} = \frac{1}{2} \left( \frac{1}{1 - x^2} + \frac{1}{1 + x^2} \right)$
因此 $\int \frac{\mathrm{d}x}{1 - x^4} = \frac{1}{2} \int \frac{\mathrm{d}x}{1 - x^2} + \frac{1}{2} \int \frac{\mathrm{d}x}{1 + x^2}$
接下来应该如何处理这两个积分呢?

第5步

对于 $\int \frac{\mathrm{d}x}{1 + x^2}$,我们可以直接套用公式,得到 $\arctan x$
将所有部分合并,得到最终答案 $$ \int \frac{\mathrm{d}x}{x^2(1 - x^4)} = -\frac{1}{x} + \frac{1}{2} \ln \left| \frac{1 + x}{1 - x} \right| - \frac{1}{2} \arctan x + C $$

1.3 $\int\frac{\mathrm{d}x}{x^4(1+x^2)}$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先排除分部法,因为分部法是针对被积函数中,含有两种或以上不同类型函数相乘的题目.而这道题的被积函数是单一的分式,不涉及不同类型函数相乘
再排除第二类换元法,因为它是针对整体无法拆分成几个部分的无理式.这道题不含无理式
因此初步判断,此题属于恒等变形+第一类换元法
你觉得应该如何变形,来寻找换元的部分呢?

第2步

观察题目发现分母中$x^4$和$1+x^2$可以通过倒代换简化
因此先尝试使用倒代换,即令 $x=\frac{1}{t}$, 则 $dx=-\frac{1}{t^2}dt$
将倒代换代入原式,得 $$ \int \frac{\mathrm{d}x}{x^4(1+x^2)} = \int \frac{-\frac{1}{t^2}dt}{(\frac{1}{t})^4(1+(\frac{1}{t})^2)} = -\int \frac{t^4}{1+t^2} dt $$
现在可以如何进一步处理这个积分呢?

第3步

观察新的被积函数 $-\int \frac{t^4}{1+t^2} dt$
可以将被积函数拆分成两部分,即 $\frac{t^4}{1+t^2} = \frac{t^4-1+1}{1+t^2} = \frac{t^4-1}{1+t^2} + \frac{1}{1+t^2}$
因此 $$ -\int \frac{t^4}{1+t^2} dt = -\int \frac{t^4-1}{1+t^2} dt - \int \frac{1}{1+t^2} dt $$
现在可以如何分别积分这两个部分呢?

第4步

对于第一部分 $\int \frac{t^4-1}{1+t^2} dt$, 可以进一步拆分成 $\int (t^2-1) dt$
因此 $$ -\int \frac{t^4-1}{1+t^2} dt = -\int (t^2-1) dt = -\left(\frac{t^3}{3} - t\right) $$
对于第二部分 $\int \frac{1}{1+t^2} dt$, 这是一个常见的积分,结果是 $\arctan t$
因此 $$ -\int \frac{1}{1+t^2} dt = -\arctan t $$
将两部分结果合并,得 $$ -\left(\frac{t^3}{3} - t - \arctan t\right) $$
最后要把换元的部分代回原式,你能完成剩余的部分吗?

第5步

换元代回原式并整理,得 $$ -\left(\frac{t^3}{3} - t - \arctan t\right) + C = -\frac{1}{3x^3} + \frac{1}{x} - \arctan \frac{1}{x} + C $$
因此,最终答案是 $$ \int \frac{\mathrm{d}x}{x^4(1+x^2)} = -\frac{1}{3x^3} + \frac{1}{x} - \arctan \frac{1}{x} + C $$

1.4 $\int \frac{\arctan x}{x^2(1 + x^2)} \mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数，它包含幂函数 $x^2$ 和反三角函数 $\arctan x$，属于两种不同类型的函数相乘
因此初步判断，此题属于恒等变形+分部法
你觉得应该如何变形，来准备使用分部积分法呢?

第2步

观察分母 $x^2(1 + x^2)$，可以进行裂项，即 $\frac{1}{x^2(1 + x^2)} = \frac{1}{x^2} - \frac{1}{1 + x^2}$
因此，原积分可以拆分为两个部分： $$ \int \frac{\arctan x}{x^2(1 + x^2)} \mathrm{d}x = \int \frac{\arctan x}{x^2} \mathrm{d}x - \int \frac{\arctan x}{1 + x^2} \mathrm{d}x $$
接下来应该如何分别处理这两个积分呢?

第3步

对于第一个积分 $\int \frac{\arctan x}{x^2} \mathrm{d}x$，可以使用分部积分法
设 $u = \arctan x$，$dv = \frac{1}{x^2} \mathrm{d}x$，则 $du = \frac{1}{1 + x^2} \mathrm{d}x$，$v = -\frac{1}{x}$
应用分部积分公式 $\int udv = uv - \int vdu$，得 $$ \int \frac{\arctan x}{x^2} \mathrm{d}x = -\frac{\arctan x}{x} + \int \frac{1}{x(1 + x^2)} \mathrm{d}x $$
对于第二个积分 $\int \frac{\arctan x}{1 + x^2} \mathrm{d}x$，同样使用分部积分法
设 $u = \arctan x$，$dv = \frac{1}{1 + x^2} \mathrm{d}x$，则 $du = \frac{1}{1 + x^2} \mathrm{d}x$，$v = \arctan x$
应用分部积分公式，得 $$ \int \frac{\arctan x}{1 + x^2} \mathrm{d}x = \frac{1}{2} (\arctan x)^2 $$
现在将两个部分的结果合并，你能完成剩余的部分吗?

第4步

合并两个部分的结果，得 $$ \int \frac{\arctan x}{x^2(1 + x^2)} \mathrm{d}x = -\frac{\arctan x}{x} + \int \frac{1}{x(1 + x^2)} \mathrm{d}x - \frac{1}{2} (\arctan x)^2 $$
对于积分 $\int \frac{1}{x(1 + x^2)} \mathrm{d}x$，可以进行裂项，即 $\frac{1}{x(1 + x^2)} = \frac{1}{x} - \frac{x}{1 + x^2}$
因此 $$ \int \frac{1}{x(1 + x^2)} \mathrm{d}x = \int \frac{1}{x} \mathrm{d}x - \int \frac{x}{1 + x^2} \mathrm{d}x = \ln |x| - \frac{1}{2} \ln (1 + x^2) $$
最终结果为 $$ \int \frac{\arctan x}{x^2(1 + x^2)} \mathrm{d}x = -\frac{\arctan x}{x} - \frac{1}{2} (\arctan x)^2 + \frac{1}{2} \ln \frac{x^2}{1 + x^2} + C $$

1.5 $\int\frac{x+\ln(1-x)}{x^2}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数 $\frac{x+\ln(1-x)}{x^2}$，它包含幂函数和对数函数两种类型的函数
因此，初步判断此题属于恒等变形+分部法
你觉得应该如何变形,来准备使用分部积分法呢?

第2步

首先对被积函数进行裂项，即 $\int\frac{x+\ln(1-x)}{x^2}\mathrm{d}x = \int\frac{x}{x^2}\mathrm{d}x + \int\frac{\ln(1-x)}{x^2}\mathrm{d}x$
简化第一项，得到 $\int\frac{1}{x}\mathrm{d}x$，这是一个基本积分，可以直接得到结果 $\ln|x|$
第二项 $\int\frac{\ln(1-x)}{x^2}\mathrm{d}x$ 需要使用分部积分法，根据口诀反对幂三指,依次当u使，选择 $\ln(1-x)$ 作为 $u$，$\frac{1}{x^2}\mathrm{d}x$ 作为 $dv$
接下来应该如何进行分部积分呢?

第3步

设 $u = \ln(1-x)$，$dv = \frac{1}{x^2}\mathrm{d}x$
计算 $du = \frac{1}{1-x}\mathrm{d}x$，$v = -\frac{1}{x}$
使用分部积分公式 $\int udv = uv - \int vdu$，得到 $$ \int\frac{\ln(1-x)}{x^2}\mathrm{d}x = -\frac{\ln(1-x)}{x} - \int-\frac{1}{x}\cdot\frac{1}{1-x}\mathrm{d}x $$
简化后得到 $$ \int\frac{\ln(1-x)}{x^2}\mathrm{d}x = -\frac{\ln(1-x)}{x} + \int\frac{1}{x(1-x)}\mathrm{d}x $$
现在需要计算 $\int\frac{1}{x(1-x)}\mathrm{d}x$，应该如何处理呢?

第4步

对 $\int\frac{1}{x(1-x)}\mathrm{d}x$ 进行裂项，即 $\frac{1}{x(1-x)} = \frac{1}{x} + \frac{1}{1-x}$
因此 $$ \int\frac{1}{x(1-x)}\mathrm{d}x = \int\frac{1}{x}\mathrm{d}x + \int\frac{1}{1-x}\mathrm{d}x $$
这两个积分都是基本积分，可以直接得到结果 $$ \int\frac{1}{x}\mathrm{d}x = \ln|x|，\int\frac{1}{1-x}\mathrm{d}x = -\ln|1-x| $$
将这些结果代入之前的表达式，你能完成剩余的部分吗?

第5步

将所有部分合并，得到 $$ \int\frac{x+\ln(1-x)}{x^2}\mathrm{d}x = \ln|x| - \frac{\ln(1-x)}{x} + \ln|x| - \ln|1-x| + C $$
进一步简化，得到 $$ \int\frac{x+\ln(1-x)}{x^2}\mathrm{d}x = \left(1 - \frac{1}{x}\right)\ln(1-x) + C $$
这样就完成了整个积分的计算

2.求积分

2.1 $\int\frac{\mathrm{d}x}{x(1+\sqrt{x})}$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察题目，被积函数中含有无理式 $\sqrt{x}$，因此考虑使用第二类换元法来消除无理式。
由于被积函数中没有不同类型函数相乘的情况，排除分部法。
初步判断，此题属于恒等变形+第二类换元法。
你觉得应该如何进行换元，来消除无理式呢？

第2步

为了消除无理式 $\sqrt{x}$，可以令 $\sqrt{x}=t$，则 $x=t^2$。
接下来需要将 $dx$ 用 $dt$ 表示出来，即 $dx = d(t^2) = 2t \, dt$。
将换元代入原式，得 $$ \int \frac{\mathrm{d}x}{x(1+\sqrt{x})} = \int \frac{2t \, dt}{t^2(1+t)} $$
现在应该如何化简这个积分呢？

第3步

化简被积函数，分子分母同时除以 $t$，得 $$ \int \frac{2t \, dt}{t^2(1+t)} = \int \frac{2 \, dt}{t(1+t)} $$
接下来需要对分式 $\frac{2}{t(1+t)}$ 进行裂项。
使用裂项法，将 $\frac{2}{t(1+t)}$ 拆分为两个部分，即 $$ \frac{2}{t(1+t)} = 2 \left( \frac{1}{t} - \frac{1}{1+t} \right) $$
将裂项后的表达式代入积分，得 $$ \int \frac{2 \, dt}{t(1+t)} = 2 \int \left( \frac{1}{t} - \frac{1}{1+t} \right) dt $$
现在可以直接积分，得 $$ 2 \int \left( \frac{1}{t} - \frac{1}{1+t} \right) dt = 2 (\ln |t| - \ln |1+t|) + C $$
最后要把换元的部分代回原式，你能完成剩余的部分吗？

第4步

将 $t = \sqrt{x}$ 代回原式，得 $$ 2 (\ln |t| - \ln |1+t|) + C = 2 (\ln |\sqrt{x}| - \ln |1+\sqrt{x}|) + C $$
进一步化简，得 $$ 2 (\ln |\sqrt{x}| - \ln |1+\sqrt{x}|) + C = 2 \ln \left| \frac{\sqrt{x}}{1+\sqrt{x}} \right| + C $$
因此，最终答案为 $$ \int \frac{\mathrm{d}x}{x(1+\sqrt{x})} = 2 \ln \frac{\sqrt{x}}{1+\sqrt{x}} + C $$

2.2 $\int\frac{x\mathrm{e}^x}{\sqrt{\mathrm{e}^x-1}}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数，发现含有无理式 $\sqrt{\mathrm{e}^x-1}$，因此考虑使用第二类换元法来消除无理式。
由于被积函数中含有 $x$ 和 $\mathrm{e}^x$ 的乘积，且 $\mathrm{e}^x$ 与 $\sqrt{\mathrm{e}^x-1}$ 相关，初步判断可以使用分部法。
因此，此题可能需要结合第二类换元法和分部法来解决。
你觉得应该如何进行换元呢？

第2步

为了消除无理式 $\sqrt{\mathrm{e}^x-1}$，可以令 $t = \sqrt{\mathrm{e}^x-1}$，即 $t^2 = \mathrm{e}^x - 1$。
由此可得 $\mathrm{e}^x = t^2 + 1$，进而 $x = \ln(t^2 + 1)$。
计算 $\mathrm{d}x$：$\mathrm{d}x = \frac{2t}{t^2 + 1} \mathrm{d}t$。
将这些代入原积分，得到新的积分形式： $$ \int \frac{x \mathrm{e}^x}{\sqrt{\mathrm{e}^x-1}} \mathrm{d}x = \int \frac{\ln(t^2 + 1) \cdot (t^2 + 1)}{t} \cdot \frac{2t}{t^2 + 1} \mathrm{d}t = 2 \int \ln(t^2 + 1) \mathrm{d}t $$
接下来应该如何处理这个积分呢？

第3步

观察到新的积分 $2 \int \ln(t^2 + 1) \mathrm{d}t$ 中含有对数函数和幂函数，适合使用分部法。
根据分部法的口诀反对幂三指,依次当u使，选择 $u = \ln(t^2 + 1)$ 和 $\mathrm{d}v = \mathrm{d}t$。
计算 $u$ 和 $\mathrm{d}v$： $$ u = \ln(t^2 + 1), \quad \mathrm{d}u = \frac{2t}{t^2 + 1} \mathrm{d}t, \quad v = t $$
使用分部积分公式 $\int u \mathrm{d}v = uv - \int v \mathrm{d}u$，得到： $$ 2 \int \ln(t^2 + 1) \mathrm{d}t = 2 \left( t \ln(t^2 + 1) - \int t \cdot \frac{2t}{t^2 + 1} \mathrm{d}t \right) $$
进一步简化： $$ 2 \left( t \ln(t^2 + 1) - 2 \int \frac{t^2}{t^2 + 1} \mathrm{d}t \right) $$
如何处理 $\int \frac{t^2}{t^2 + 1} \mathrm{d}t$ 呢？

第4步

观察到 $\frac{t^2}{t^2 + 1}$ 可以进行裂项： $$ \frac{t^2}{t^2 + 1} = 1 - \frac{1}{t^2 + 1} $$
因此： $$ \int \frac{t^2}{t^2 + 1} \mathrm{d}t = \int 1 \mathrm{d}t - \int \frac{1}{t^2 + 1} \mathrm{d}t = t - \arctan t + C $$
代入回原积分： $$ 2 \left( t \ln(t^2 + 1) - 2 (t - \arctan t) \right) $$
进一步简化： $$ 2 t \ln(t^2 + 1) - 4 t + 4 \arctan t + C $$
最后将 $t$ 换回原变量 $x$： $$ 2 x \sqrt{\mathrm{e}^x - 1} - 4 \sqrt{\mathrm{e}^x - 1} + 4 \arctan \sqrt{\mathrm{e}^x - 1} + C $$

第5步

总结整个过程，原积分的解为： $$ \int \frac{x \mathrm{e}^x}{\sqrt{\mathrm{e}^x-1}} \mathrm{d}x = 2 x \sqrt{\mathrm{e}^x-1} - 4 \sqrt{\mathrm{e}^x-1} + 4 \arctan \sqrt{\mathrm{e}^x-1} + C $$

2.3 $\int\frac{x^3}{\sqrt{1+x^2}}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察题目中含有无理式 $\sqrt{1+x^2}$，这表明需要使用第二类换元法来消除无理式
由于根号内是 $x^2$，根据知识点，应该使用三角代换，具体来说，令 $x=\tan t$，其中 $t \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$
你觉得应该如何进行换元呢?

第2步

令 $x=\tan t$，则 $\mathrm{d}x=\sec^2 t \mathrm{d}t$
将换元代入原式，得到 $$ \int \frac{x^3}{\sqrt{1+x^2}} \mathrm{d}x = \int \frac{\tan^3 t \cdot \sec^2 t}{\sec t} \mathrm{d}t $$
化简被积函数，得到 $$ \int \tan^2 t \cdot \sec t \mathrm{d}t $$
接下来应该如何处理这个积分呢?

第3步

注意到 $\tan^2 t = \sec^2 t - 1$，所以被积函数可以改写为 $$ \int (\sec^2 t - 1) \sec t \mathrm{d}t $$
这可以分成两个积分 $$ \int \sec^3 t \mathrm{d}t - \int \sec t \mathrm{d}t $$
这两个积分都是基本积分表中的公式，可以直接求解
你能完成这两个积分的计算吗?

第4步

计算 $\int \sec^3 t \mathrm{d}t$ 和 $\int \sec t \mathrm{d}t$
$\int \sec^3 t \mathrm{d}t = \frac{1}{2} \sec t \tan t + \frac{1}{2} \ln |\sec t + \tan t| + C_1$
$\int \sec t \mathrm{d}t = \ln |\sec t + \tan t| + C_2$
将这两个结果代入，得到 $$ \int \tan^2 t \cdot \sec t \mathrm{d}t = \frac{1}{2} \sec t \tan t + \frac{1}{2} \ln |\sec t + \tan t| - \ln |\sec t + \tan t| + C $$
化简后得到 $$ \int \tan^2 t \cdot \sec t \mathrm{d}t = \frac{1}{2} \sec t \tan t - \frac{1}{2} \ln |\sec t + \tan t| + C $$
最后要把换元的部分代回原式，你能完成剩余的部分吗?

第5步

还原换元，$\sec t = \sqrt{1+x^2}$，$\tan t = x$
代入后得到 $$ \int \frac{x^3}{\sqrt{1+x^2}} \mathrm{d}x = \frac{1}{2} x \sqrt{1+x^2} - \frac{1}{2} \ln |\sqrt{1+x^2} + x| + C $$
这是最终的积分结果

2.4 $\int\frac{\mathrm{d}x}{(2x^2+1)\sqrt{1+x^2}}$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察题目，被积函数中含有无理式 $\sqrt{1+x^2}$，这表明需要使用第二类换元法中的三角代换来消除无理式。
由于根号内是 $x^2$，根据知识点，应该选择三角代换中的tan代换。
因此，初步判断此题属于第二类换元法。
你觉得应该如何进行代换呢?

第2步

令 $x = \tan t$，则 $\mathrm{d}x = \sec^2 t \mathrm{d}t$。
将 $x = \tan t$ 和 $\mathrm{d}x = \sec^2 t \mathrm{d}t$ 代入原积分，得到 $$ \int \frac{\mathrm{d}x}{(2x^2+1)\sqrt{1+x^2}} = \int \frac{\sec^2 t \mathrm{d}t}{(2\tan^2 t + 1)\sec t} $$
进一步化简，得到 $$ \int \frac{\sec^2 t \mathrm{d}t}{(2\tan^2 t + 1)\sec t} = \int \frac{\cos t \mathrm{d}t}{2\sin^2 t + \cos^2 t} $$
现在应该如何继续化简呢?

第3步

注意到 $2\sin^2 t + \cos^2 t = 1 + \sin^2 t$，所以积分变为 $$ \int \frac{\cos t \mathrm{d}t}{1 + \sin^2 t} $$
接下来可以使用第一类换元法，将 $\cos t \mathrm{d}t$ 看作 $\mathrm{d}(\sin t)$，即 $$ \int \frac{\cos t \mathrm{d}t}{1 + \sin^2 t} = \int \frac{\mathrm{d}(\sin t)}{1 + \sin^2 t} $$
这个积分是一个常见的积分形式，可以直接得到结果。
你能完成这个积分吗?

第4步

根据基本积分公式，$\int \frac{\mathrm{d}u}{1 + u^2} = \arctan u + C$，所以 $$ \int \frac{\mathrm{d}(\sin t)}{1 + \sin^2 t} = \arctan (\sin t) + C $$
现在需要将 $\sin t$ 代回原变量 $x$。
由于 $x = \tan t$，所以 $\sin t = \frac{x}{\sqrt{1+x^2}}$。
你能完成最后的代换吗?

第5步

将 $\sin t = \frac{x}{\sqrt{1+x^2}}$ 代入结果，得到 $$ \arctan (\sin t) + C = \arctan \left(\frac{x}{\sqrt{1+x^2}}\right) + C $$
因此，原积分的最终结果是 $$ \int \frac{\mathrm{d}x}{(2x^2+1)\sqrt{1+x^2}} = \arctan \left(\frac{x}{\sqrt{1+x^2}}\right) + C $$

2.5 $\int\frac{\arctan\sqrt{x-1}}{x\:\sqrt{x-1}}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察题目，被积函数中含有无理式 $\sqrt{x-1}$，因此考虑使用第二类换元法来消除无理式。
由于被积函数中还含有反三角函数 $\arctan\sqrt{x-1}$，初步判断此题可能需要分部法。
你觉得应该如何进行换元，来消除无理式呢？

第2步

为了消除无理式 $\sqrt{x-1}$，可以令 $t = \sqrt{x-1}$，即 $t^2 = x-1$，从而 $x = t^2 + 1$。
接下来计算 $dx$： $$ dx = d(t^2 + 1) = 2t \, dt $$
将换元代入原式并作化简： $$ \int \frac{\arctan t}{(t^2 + 1) t} \cdot 2t \, dt = 2 \int \frac{\arctan t}{t^2 + 1} \, dt $$
现在被积函数中已经没有无理式了，接下来应该如何处理呢？

第3步

观察新的被积函数 $2 \int \frac{\arctan t}{t^2 + 1} \, dt$，注意到 $\frac{d}{dt} \arctan t = \frac{1}{t^2 + 1}$。
因此可以进行凑微分： $$ 2 \int \frac{\arctan t}{t^2 + 1} \, dt = 2 \int \arctan t \, d(\arctan t) $$ 如果没有注意到凑微分,也可以直接使用分部积分法.根据口诀,将$\arctan t$看作u,剩余部分看作$dv$,也能发现上述凑微分的部分,计算过程与上述过程一样.
现在可以直接积分，得： $$ 2 \int \arctan t \, d(\arctan t) = 2 \cdot \frac{1}{2} (\arctan t)^2 + C = (\arctan t)^2 + C $$
最后要把换元的部分代回原式，你能完成剩余的部分吗？

第4步

换元代回原式并整理，得： $$ (\arctan t)^2 + C = (\arctan \sqrt{x-1})^2 + C $$
因此，原积分的解为： $$ \int \frac{\arctan \sqrt{x-1}}{x \sqrt{x-1}} \, dx = (\arctan \sqrt{x-1})^2 + C $$

2.6 $\int\sqrt\frac{x}{1-x\sqrt{x}}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察题目，发现含有无理式，因此考虑使用第二类换元法。
题目中的无理式是 $\sqrt{x}$ 和 $\sqrt{x \sqrt{x}}$，这属于无理代换的范畴。
你觉得应该如何选择代换，来消除无理式呢？

第2步

观察被积函数 $\sqrt{\frac{x}{1-x \sqrt{x}}}$，注意到分母中的 $\sqrt{x \sqrt{x}}$ 可以写成 $x^{\frac{3}{2}}$。
因此，考虑令 $u = x^{\frac{3}{2}}$，这样可以将无理式转化为有理式。
接下来应该如何进行代换呢？

第3步

令 $u = x^{\frac{3}{2}}$，则 $x = u^{\frac{2}{3}}$，即 $dx = \frac{2}{3} {u^{-\frac{1}{3}}}du$。
且,可以将 $x^{\frac{1}{2}}$ 表示为 $u^{\frac{1}{3}}$。
将这些代入原式，得到 $$ \int \sqrt{\frac{x}{1-x \sqrt{x}}} \mathrm{~d} x = \int \frac{\sqrt{x}}{\sqrt{1-x \sqrt{x}}} \mathrm{~d} x = \int \frac{\cancel{u^{\frac{1}{3}}}}{\sqrt{1-u}} \cdot \frac{2}{3} \cancel{{u^{-\frac{1}{3}}}}du $$
化简后得到 $$ \frac{2}{3} \int \frac{1}{\sqrt{1-u}} du $$
剩下的积分应该如何计算呢？

第4步

注意到 $\int \frac{1}{\sqrt{1-u}} du$ 是一个常见的积分，可以利用基本积分公式 $\int (1-u)^{-\frac{1}{2}} du = -2 \sqrt{1-u}$。
因此 $$ \frac{2}{3} \int \frac{1}{\sqrt{1-u}} du = \frac{2}{3} \cdot (-2) \sqrt{1-u} = -\frac{4}{3} \sqrt{1-u} $$
最后要把换元的部分代回原式，你能完成剩余的部分吗？

第5步

换元代回原式并整理，得 $$ -\frac{4}{3} \sqrt{1-x^{\frac{3}{2}}} + C $$
因此，最终答案是 $$ \int \sqrt{\frac{x}{1-x \sqrt{x}}} \mathrm{~d} x = -\frac{4}{3} \sqrt{1-x \sqrt{x}} + C $$

3.求积分

3.1 $\int\frac{\mathrm{d}x}{\sin^2x\cos^4x}$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先排除分部法,因为分部法是针对被积函数中,含有两种或以上不同类型函数相乘的题目.而这道题的被积函数是三角函数的有理式,即只有一种类型的函数
再排除第二类换元法,因为它是针对整体无法拆分成几个部分的无理式.这道题不含无理式
因此初步判断,此题属于恒等变形+第一类换元法
你觉得应该如何变形,来寻找换元的部分呢?

第2步

观察题目发现被积函数是三角函数的有理式
因此先尝试利用三角恒等式进行变形,即 $\int \frac{1}{\sin ^2 x \cos ^4 x} \mathrm{~d} x=\int \frac{\left(\sin ^2 x+\cos ^2 x\right)^2}{\sin ^2 x \cos ^4 x} \mathrm{~d} x$
利用 $\sin ^2 x+\cos ^2 x=1$, 可以将分子展开,即 $\int \frac{1}{\sin ^2 x \cos ^4 x} \mathrm{~d} x=\int\left(\frac{\sin ^2 x}{\cos ^4 x}+\frac{2}{\cos ^2 x}+\frac{1}{\sin ^2 x}\right) \mathrm{d} x$
现在可以分别对每一项进行积分,你能完成剩余的部分吗?

第3步

对于第一项 $\int \frac{\sin ^2 x}{\cos ^4 x} \mathrm{~d} x$, 可以令 $u=\tan x$, 则 $\mathrm{d}u=\frac{1}{\cos^2 x} \mathrm{d}x$
因此 $\int \frac{\sin ^2 x}{\cos ^4 x} \mathrm{~d} x=\int \tan ^2 x \mathrm{~d}(\tan x)=\int u^2 \mathrm{d}u=\frac{1}{3}u^3+C_1=\frac{1}{3}\tan^3 x+C_1$
对于第二项 $\int \frac{2}{\cos ^2 x} \mathrm{~d} x$, 可以直接积分,得 $2\int \sec^2 x \mathrm{~d} x=2\tan x+C_2$
对于第三项 $\int \frac{1}{\sin ^2 x} \mathrm{~d} x$, 可以直接积分,得 $-\int \csc^2 x \mathrm{~d} x=-\cot x+C_3$
将各项结果相加,得 $\frac{1}{3}\tan^3 x+2\tan x-\cot x+C$

第4步

另一种方法是分子、分母同乘以 $\cos ^2 x$, 得 $\int \frac{1}{\sin ^2 x \cos ^4 x} \mathrm{~d} x=\int \frac{\cos^2 x}{\sin ^2 x \cos ^6 x} \mathrm{~d} x=\int \frac{\sec^4 x}{\tan ^2 x} \mathrm{~d}(\tan x)$
利用 $\sec^2 x=1+\tan^2 x$, 可以将分子展开,即 $\int \frac{\sec^4 x}{\tan ^2 x} \mathrm{~d}(\tan x)=\int \frac{\tan^4 x+2\tan^2 x+1}{\tan ^2 x} \mathrm{~d}(\tan x)$
将分子拆开,得 $\int \left(\tan^2 x+2+\frac{1}{\tan^2 x}\right) \mathrm{~d}(\tan x)$
分别对每一项进行积分,得 $\frac{1}{3}\tan^3 x+2\tan x-\cot x+C$

第5步

通过上述两种方法,都可以得到相同的结果 $\frac{1}{3}\tan^3 x+2\tan x-\cot x+C$
这表明两种方法都是正确的,可以根据个人喜好选择其中一种方法进行计算

3.2 $\int\frac{\mathrm{d}x}{1+\sin x}$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先排除分部法,因为分部法是针对被积函数中,含有两种或以上不同类型函数相乘的题目.而这道题的被积函数是单一的三角函数,即只有一种类型的函数
再排除第二类换元法,因为它是针对整体无法拆分成几个部分的无理式.这道题不含无理式
因此初步判断,此题属于恒等变形+第一类换元法
你觉得应该如何变形,来寻找换元的部分呢?

第2步

观察题目发现分母是 $1+\sin x$
为了简化分母,可以尝试分子分母同时乘以 $1-\sin x$,即 $$ \int \frac{1}{1+\sin x} \mathrm{~d} x = \int \frac{1-\sin x}{(1+\sin x)(1-\sin x)} \mathrm{~d} x $$
这样做的目的是什么?

第3步

通过分子分母同时乘以 $1-\sin x$,分母变为 $1-\sin^2 x$,即 $\cos^2 x$
因此积分变为 $$ \int \frac{1-\sin x}{\cos^2 x} \mathrm{~d} x $$
现在可以拆分成两个积分,即 $$ \int \frac{1}{\cos^2 x} \mathrm{~d} x - \int \frac{\sin x}{\cos^2 x} \mathrm{~d} x $$
这两个积分应该如何计算呢?

第4步

第一个积分 $\int \frac{1}{\cos^2 x} \mathrm{~d} x$ 是常见的基本积分,结果是 $\tan x$
第二个积分 $\int \frac{\sin x}{\cos^2 x} \mathrm{~d} x$ 可以通过换元法计算,令 $u = \cos x$,则 $\mathrm{d}u = -\sin x \mathrm{d}x$,即 $$ \int \frac{\sin x}{\cos^2 x} \mathrm{~d} x = -\int \frac{1}{u^2} \mathrm{~d}u = \frac{1}{u} = \frac{1}{\cos x} $$
因此原积分的结果是 $$ \int \frac{1}{1+\sin x} \mathrm{~d} x = \tan x - \frac{1}{\cos x} + C $$

3.3 $\int\frac{\sin x}{\sin x+\cos x}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数 $\frac{\sin x}{\sin x+\cos x}$，它包含两种不同类型的函数：三角函数和三角函数相加。
由于被积函数是两种不同类型函数的组合，初步判断可能适用分部法。
但是，直接使用分部法可能不太方便，因为我们需要找到一种方法将分子和分母更好地结合起来。
因此，考虑使用恒等变形来简化被积函数，然后再使用换元法或分部法。
你觉得应该如何变形，来寻找换元的部分呢?

第2步

观察题目，我们可以利用三角函数的性质来进行恒等变形。
具体来说，我们可以将被积函数拆分成两个部分，使得每一部分都可以更容易地积分。
利用公式 $f(x) = \frac{f(x) + f(-x)}{2} + \frac{f(x) - f(-x)}{2}$，我们可以将被积函数拆分成一个偶函数和一个奇函数之和。
具体操作如下： $$ \int \frac{\sin x}{\sin x + \cos x} \mathrm{d} x = \frac{1}{2} \int \frac{(\sin x + \cos x) + (\sin x - \cos x)}{\sin x + \cos x} \mathrm{d} x $$
这样，我们可以将积分拆分成两个部分： $$ \frac{1}{2} \int \frac{\sin x + \cos x}{\sin x + \cos x} \mathrm{d} x + \frac{1}{2} \int \frac{\sin x - \cos x}{\sin x + \cos x} \mathrm{d} x $$
接下来应该如何处理这两个积分呢?

第3步

对于第一个积分 $\frac{1}{2} \int \frac{\sin x + \cos x}{\sin x + \cos x} \mathrm{d} x$，显然可以直接积分： $$ \frac{1}{2} \int \frac{\sin x + \cos x}{\sin x + \cos x} \mathrm{d} x = \frac{1}{2} \int 1 \mathrm{d} x = \frac{1}{2} x $$
对于第二个积分 $\frac{1}{2} \int \frac{\sin x - \cos x}{\sin x + \cos x} \mathrm{d} x$，我们可以使用换元法。
令 $u = \sin x + \cos x$，则 $\mathrm{d} u = (\cos x - \sin x) \mathrm{d} x$，即 $\mathrm{d} u = -(\sin x - \cos x) \mathrm{d} x$。
因此，第二个积分可以写成： $$ \frac{1}{2} \int \frac{\sin x - \cos x}{\sin x + \cos x} \mathrm{d} x = -\frac{1}{2} \int \frac{\mathrm{d} u}{u} = -\frac{1}{2} \ln |u| $$
最后要把换元的部分代回原式，你能完成剩余的部分吗?

第4步

换元代回原式并整理，得： $$ \int \frac{\sin x}{\sin x + \cos x} \mathrm{d} x = \frac{1}{2} x - \frac{1}{2} \ln |\sin x + \cos x| + C $$

3.4 $\int\frac{3\sin x+\cos x}{\sin x+2\cos x}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先排除换元法,因为换元法是针对被积函数中,含有整体无法拆分的无理式的题目.而这道题的被积函数是三角函数,不含无理式
因此初步判断,此题属于恒等变形+分部法
你觉得应该如何变形,来寻找分部的部分呢?

第2步

观察题目发现被积函数是两个三角函数相除的形式
因此先尝试把分子拆分成与分母相关的形式,即 $3 \sin x+\cos x=A(\sin x+2 \cos x)+B(\cos x-2 \sin x)$
通过比较两边系数, 可得 $A=1, B=-1$
接下来应该如何代换呢?

第3步

将拆分的结果代入原式,得 $$ \int \frac{3 \sin x+\cos x}{\sin x+2 \cos x} \mathrm{~d} x = \int \frac{(\sin x+2 \cos x)-(\cos x-2 \sin x)}{\sin x+2 \cos x} \mathrm{~d} x $$
现在可以将其拆分成两个积分,得 $$ \int \frac{\sin x+2 \cos x}{\sin x+2 \cos x} \mathrm{~d} x - \int \frac{\cos x-2 \sin x}{\sin x+2 \cos x} \mathrm{~d} x $$
第一个积分可以直接得到结果,第二个积分可以通过凑微分法来求解,你能完成剩余的部分吗?

第4步

第一个积分的结果是 $x$
第二个积分可以通过凑微分法,即 $\int \frac{\cos x-2 \sin x}{\sin x+2 \cos x} \mathrm{~d} x = -\int \frac{\mathrm{d}(\sin x+2 \cos x)}{\sin x+2 \cos x}$
现在可以直接积分,得 $$ -\int \frac{\mathrm{d}(\sin x+2 \cos x)}{\sin x+2 \cos x} = -\ln |\sin x+2 \cos x| $$
最后将两个积分结果相加,得 $$ x - \ln |\sin x+2 \cos x| + C $$

第5步

综上所述,原积分的解为 $$ \int \frac{3 \sin x+\cos x}{\sin x+2 \cos x} \mathrm{~d} x = x - \ln |\sin x+2 \cos x| + C $$

3.5 $\int\frac{\mathrm{d}x}{\sin2x+2\sin x}$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先排除分部法,因为分部法是针对被积函数中,含有两种或以上不同类型函数相乘的题目.而这道题的被积函数是三角函数,属于单一类型的函数
再排除第二类换元法,因为它是针对整体无法拆分成几个部分的无理式.这道题不含无理式
因此初步判断,此题属于恒等变形+第一类换元法
你觉得应该如何变形,来寻找换元的部分呢?

第2步

观察题目发现被积函数中含有$\sin 2x$和$\sin x$
因此先尝试把$\sin 2x$用$\sin x$和$\cos x$表示,即 $\sin 2x = 2 \sin x \cos x$
这样原式变为 $\int \frac{\mathrm{d}x}{2 \sin x \cos x + 2 \sin x}$
为了简化表达,可以提取公因子,即 $\int \frac{\mathrm{d}x}{2 \sin x (1 + \cos x)}$
现在可以考虑使用万能代换,即令 $\tan \frac{x}{2} = t$
接下来应该如何代换呢?

第3步

使用万能代换,令 $\tan \frac{x}{2} = t$, 则 $\sin x = \frac{2t}{1+t^2}$, $\cos x = \frac{1-t^2}{1+t^2}$, $\mathrm{d}x = \frac{2 \mathrm{d}t}{1+t^2}$
将这些代入原式,得 $$ \int \frac{\mathrm{d}x}{2 \sin x (1 + \cos x)} = \int \frac{\frac{2 \mathrm{d}t}{1+t^2}}{2 \cdot \frac{2t}{1+t^2} \cdot \left(1 + \frac{1-t^2}{1+t^2}\right)} $$
化简分母,得 $$ \int \frac{\frac{2 \mathrm{d}t}{1+t^2}}{2 \cdot \frac{2t}{1+t^2} \cdot \frac{2}{1+t^2}} = \int \frac{\frac{2 \mathrm{d}t}{1+t^2}}{\frac{8t}{1+t^2}} = \int \frac{1+t^2}{4t} \mathrm{d}t $$
剩下的积分应该如何计算呢?

第4步

$\int \frac{1+t^2}{4t} \mathrm{d}t$ 可以拆分成两个积分,即 $$ \int \frac{1+t^2}{4t} \mathrm{d}t = \frac{1}{4} \int \frac{1}{t} \mathrm{d}t + \frac{1}{4} \int t \mathrm{d}t $$
现在可以直接积分,得 $$ \frac{1}{4} \ln |t| + \frac{1}{8} t^2 + C $$
最后要把换元的部分代回原式,你能完成剩余的部分吗?

第5步

换元代回原式并整理,得 $$ \frac{1}{4} \ln \left|\tan \frac{x}{2}\right| + \frac{1}{8} \tan^2 \frac{x}{2} + C $$

3.6 $\int\frac{\mathrm{d}x}{a^2\sin^2x+b^2\cos^2x}$ ($a^2+b^2>0$)

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先排除分部法,因为分部法是针对被积函数中,含有两种或以上不同类型函数相乘的题目.而这道题的被积函数是单一的三角函数形式,即只有一种类型的函数
再排除第二类换元法,因为它是针对整体无法拆分成几个部分的无理式.这道题不含无理式
因此初步判断,此题属于恒等变形+第一类换元法
你觉得应该如何变形,来寻找换元的部分呢?

第2步

观察题目发现被积函数中含有 $\sin^2 x$ 和 $\cos^2 x$
考虑使用三角恒等式 $\sin^2 x + \cos^2 x = 1$ 进行变形
当 $a = 0, b \neq 0$ 时, 积分变为 $\int \frac{\mathrm{d} x}{b^2 \cos^2 x} = \frac{1}{b^2} \tan x + C$
当 $a \neq 0, b = 0$ 时, 积分变为 $\int \frac{\mathrm{d} x}{a^2 \sin^2 x} = -\frac{1}{a^2} \cot x + C$
当 $a \neq 0$ 且 $b \neq 0$ 时, 可以进行如下变形: $$ \int \frac{\mathrm{d} x}{a^2 \sin^2 x + b^2 \cos^2 x} = \int \frac{\mathrm{d} x}{b^2 \cos^2 x \left(1 + \frac{a^2}{b^2} \tan^2 x\right)} $$
现在可以令 $u = \tan x$, 接下来应该如何代换呢?

第3步

$u = \tan x$, 故 $dx = \frac{1}{1 + u^2} \mathrm{d}u$
将换元代入原式并作化简,得 $$ \int \frac{\mathrm{d} x}{b^2 \cos^2 x \left(1 + \frac{a^2}{b^2} \tan^2 x\right)} = \int \frac{1}{b^2 \cos^2 x \left(1 + \frac{a^2}{b^2} u^2\right)} \cdot \frac{1}{1 + u^2} \mathrm{d}u $$
进一步化简,得 $$ \int \frac{1}{b^2 \cos^2 x \left(1 + \frac{a^2}{b^2} u^2\right)} \cdot \frac{1}{1 + u^2} \mathrm{d}u = \int \frac{1}{b^2 \left(1 + \frac{a^2}{b^2} u^2\right)} \mathrm{d}u $$
现在可以直接积分,得 $$ \int \frac{1}{b^2 \left(1 + \frac{a^2}{b^2} u^2\right)} \mathrm{d}u = \frac{1}{a b} \int \frac{1}{1 + \left(\frac{a}{b} u\right)^2} \mathrm{d}\left(\frac{a}{b} u\right) $$
剩下的积分应该如何计算呢?

第4步

$\int \frac{1}{1 + \left(\frac{a}{b} u\right)^2} \mathrm{d}\left(\frac{a}{b} u\right)$ 是一个常见的积分形式,可以直接使用反正切函数的积分公式
因此 $$ \int \frac{1}{1 + \left(\frac{a}{b} u\right)^2} \mathrm{d}\left(\frac{a}{b} u\right) = \arctan \left(\frac{a}{b} u\right) + C $$
将结果代回原变量,得 $$ \frac{1}{a b} \arctan \left(\frac{a}{b} \tan x\right) + C $$

第5步

综上所述,当 $a \neq 0$ 且 $b \neq 0$ 时,积分结果为 $$ \int \frac{\mathrm{d} x}{a^2 \sin^2 x + b^2 \cos^2 x} = \frac{1}{a b} \arctan \left(\frac{a}{b} \tan x\right) + C $$
当 $a = 0, b \neq 0$ 时,积分结果为 $\frac{1}{b^2} \tan x + C$
当 $a \neq 0, b = 0$ 时,积分结果为 $-\frac{1}{a^2} \cot x + C$

4.求积分

4.1 $\int \arctan \sqrt{x} \mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先排除恒等变形+换元法,因为恒等变形的目的是为换元法作准备,应当把变量集中到一起,有利于整体换元或局部积分.而这道题的被积函数是单个反三角函数,无法进行有效的恒等变形.
因此初步判断,此题属于分部法
你觉得应该如何选择u和dv呢?

第2步

根据分部法的口诀反对幂三指,依次当u使,反三角函数arctan \sqrt{x}应该作为u,而dx作为dv
因此,设 $u = \arctan \sqrt{x}$, $dv = dx$
接下来应该如何计算du和v呢?

第3步

$u = \arctan \sqrt{x}$, 所以 $du = \frac{1}{1+(\sqrt{x})^2} \cdot \frac{1}{2\sqrt{x}} dx = \frac{1}{2\sqrt{x}(1+x)} dx$
$dv = dx$, 所以 $v = x$
将这些代入分部积分公式 $\int udv = uv - \int vdu$, 得 $$ \int \arctan \sqrt{x} \mathrm{d}x = x \arctan \sqrt{x} - \int x \cdot \frac{1}{2\sqrt{x}(1+x)} \mathrm{d}x $$
现在应该如何处理剩下的积分呢?

第4步

剩下的积分 $\int x \cdot \frac{1}{2\sqrt{x}(1+x)} \mathrm{d}x$ 可以进行简化
首先,简化被积函数 $\frac{x}{2\sqrt{x}(1+x)} = \frac{\sqrt{x}}{2(1+x)}$
然后,考虑裂项 $\frac{\sqrt{x}}{2(1+x)} = \frac{1}{2} \left( \frac{\sqrt{x}}{1+x} \right)$
进一步简化, $\frac{\sqrt{x}}{1+x} = \frac{1+x-1}{1+x} = 1 - \frac{1}{1+x}$
因此,积分变为 $$ \int \frac{\sqrt{x}}{2(1+x)} \mathrm{d}x = \frac{1}{2} \int \left( 1 - \frac{1}{1+x} \right) \mathrm{d}x $$
现在可以直接积分,得 $$ \frac{1}{2} \left( \int 1 \mathrm{d}x - \int \frac{1}{1+x} \mathrm{d}x \right) = \frac{1}{2} \left( x - \ln|1+x| \right) $$
最后要把这些结果代回原式,你能完成剩余的部分吗?

第5步

将所有部分代回原式并整理,得 $$ \int \arctan \sqrt{x} \mathrm{d}x = x \arctan \sqrt{x} - \frac{1}{2} \left( x - \ln|1+x| \right) + C $$
进一步简化,得 $$ \int \arctan \sqrt{x} \mathrm{d}x = x \arctan \sqrt{x} - \frac{1}{2} x + \frac{1}{2} \ln|1+x| + C $$
最终答案为 $$ \int \arctan \sqrt{x} \mathrm{d}x = x \arctan \sqrt{x} - \sqrt{x} + \arctan \sqrt{x} + C $$

4.2 $\int\frac{\ln x}{(1-x)^2}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数 $\frac{\ln x}{(1-x)^2}$，它包含对数函数 $\ln x$ 和幂函数 $(1-x)^{-2}$，这属于两种不同类型的函数相乘
根据分部法的适用条件，这道题应该使用分部法
根据口诀反对幂三指,依次当u使，选择对数函数 $\ln x$ 作为 $u$，幂函数 $(1-x)^{-2}dx$ 作为 $dv$
你觉得应该如何进行分部积分呢?

第2步

设 $u = \ln x$，$dv = \frac{1}{(1-x)^2} dx$
计算 $du$ 和 $v$:
- $du = \frac{1}{x} dx$
- $v = \int \frac{1}{(1-x)^2} dx$
计算 $v$ 时，可以使用换元法，令 $y = 1 - x$，则 $dy = -dx$，所以
- $v = \int \frac{1}{y^2} (-dy) = -\int y^{-2} dy = y^{-1} = \frac{1}{1-x}$
现在可以进行分部积分，得 $$ \int \frac{\ln x}{(1-x)^2} dx = \ln x \cdot \frac{1}{1-x} - \int \frac{1}{1-x} \cdot \frac{1}{x} dx $$
你能继续简化这个积分吗?

第3步

现在我们需要计算 $\int \frac{1}{x(1-x)} dx$
这个积分可以通过裂项法来简化，即 $$ \frac{1}{x(1-x)} = \frac{1}{x} + \frac{1}{1-x} $$
因此 $$ \int \frac{1}{x(1-x)} dx = \int \frac{1}{x} dx + \int \frac{1}{1-x} dx $$
这两个积分都可以直接计算，得 $$ \int \frac{1}{x} dx = \ln |x| + C_1 $$ $$ \int \frac{1}{1-x} dx = -\ln |1-x| + C_2 $$
你能将这些结果代入原积分并整理吗?

第4步

将所有部分代入原积分并整理，得 $$ \int \frac{\ln x}{(1-x)^2} dx = \frac{\ln x}{1-x} - \left( \ln |x| - \ln |1-x| \right) + C $$
进一步简化，得 $$ \int \frac{\ln x}{(1-x)^2} dx = \frac{\ln x}{1-x} + \ln \left| \frac{1-x}{x} \right| + C $$
最终答案为 $$ \int \frac{\ln x}{(1-x)^2} dx = -\frac{\ln x}{x-1} + \ln |x-1| - \ln |x| + C $$

4.3 $\int \frac{x^2 \mathrm{e}^x}{(x + 2)^2} \mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数 $\frac{x^2 \mathrm{e}^x}{(x + 2)^2}$，它包含指数函数和幂函数，因此属于含有两种不同类型函数相乘的情况。
根据知识点，这种情况适用分部法。
你觉得应该如何选择 $u$ 和 $dv$ 呢？

第2步

根据分部法的口诀反对幂三指,依次当u使，我们选择 $u = x^2 \mathrm{e}^x$ 和 $dv = \frac{1}{(x + 2)^2} \mathrm{d}x$。
计算 $du$ 和 $v$：
- $du = (x^2 \mathrm{e}^x)' \mathrm{d}x = (2x \mathrm{e}^x + x^2 \mathrm{e}^x) \mathrm{d}x$
- $v = \int \frac{1}{(x + 2)^2} \mathrm{d}x = -\frac{1}{x + 2}$
现在应用分部积分公式 $\int udv = uv - \int vdu$，你能完成这一步吗？

第3步

应用分部积分公式： $$ \int \frac{x^2 \mathrm{e}^x}{(x + 2)^2} \mathrm{d}x = -x^2 \mathrm{e}^x \cdot \frac{1}{x + 2} + \int \frac{1}{x + 2} \cdot (2x \mathrm{e}^x + x^2 \mathrm{e}^x) \mathrm{d}x $$
简化积分： $$ = -\frac{x^2 \mathrm{e}^x}{x + 2} + \int \frac{2x \mathrm{e}^x + x^2 \mathrm{e}^x}{x + 2} \mathrm{d}x $$
你能继续简化这个积分吗？

第4步

继续简化积分： $$ = -\frac{x^2 \mathrm{e}^x}{x + 2} + \int \frac{x(2 \mathrm{e}^x + x \mathrm{e}^x)}{x + 2} \mathrm{d}x $$
进一步简化： $$ = -\frac{x^2 \mathrm{e}^x}{x + 2} + \int x \mathrm{e}^x \mathrm{d}x $$
现在需要再次使用分部法来积分 $\int x \mathrm{e}^x \mathrm{d}x$，你能完成这一步吗？

第5步

再次使用分部法，选择 $u = x$ 和 $dv = \mathrm{e}^x \mathrm{d}x$：
- $du = \mathrm{d}x$
- $v = \mathrm{e}^x$
应用分部积分公式： $$ \int x \mathrm{e}^x \mathrm{d}x = x \mathrm{e}^x - \int \mathrm{e}^x \mathrm{d}x = x \mathrm{e}^x - \mathrm{e}^x $$
将结果代入原积分： $$ \int \frac{x^2 \mathrm{e}^x}{(x + 2)^2} \mathrm{d}x = -\frac{x^2 \mathrm{e}^x}{x + 2} + x \mathrm{e}^x - \mathrm{e}^x + C $$
最终答案是： $$ \int \frac{x^2 \mathrm{e}^x}{(x + 2)^2} \mathrm{d}x = -\frac{x^2 \mathrm{e}^x}{x + 2} + x \mathrm{e}^x - \mathrm{e}^x + C $$

4.4 $\int\sin(\ln x)\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数 $\sin(\ln x)$，它包含一个三角函数和一个对数函数，但它们是嵌套的关系，而不是直接相乘的关系。
因此，初步判断此题需要先进行换元法，将嵌套关系变为相乘关系，然后再使用分部法。
你觉得应该如何进行换元呢?

第2步

令 $\ln x = t$，则 $x = e^t$，并且 $\mathrm{d}x = e^t \mathrm{d}t$。
将换元代入原式，得到 $\int \sin(\ln x) \mathrm{d}x = \int \sin t \cdot e^t \mathrm{d}t$。
现在被积函数变成了 $\sin t \cdot e^t$，这是一个三角函数和指数函数的乘积，可以使用分部法。
接下来应该如何使用分部法呢?

第3步

根据分部法的口诀反对幂三指,依次当u使，我们选择 $\sin t$ 作为 $u$，$e^t \mathrm{d}t$ 作为 $\mathrm{d}v$。
计算 $u$ 和 $\mathrm{d}v$ 的导数和积分：
- $u = \sin t$，$\mathrm{d}u = \cos t \mathrm{d}t$
- $\mathrm{d}v = e^t \mathrm{d}t$，$v = e^t$
使用分部积分公式 $\int u \mathrm{d}v = uv - \int v \mathrm{d}u$，得到： $$ \int \sin t \cdot e^t \mathrm{d}t = e^t \sin t - \int e^t \cos t \mathrm{d}t $$
现在需要计算 $\int e^t \cos t \mathrm{d}t$，应该如何进行呢?

第4步

对于 $\int e^t \cos t \mathrm{d}t$，再次使用分部法：
- 选择 $\cos t$ 作为 $u$，$e^t \mathrm{d}t$ 作为 $\mathrm{d}v$。
- $u = \cos t$，$\mathrm{d}u = -\sin t \mathrm{d}t$
- $\mathrm{d}v = e^t \mathrm{d}t$，$v = e^t$
使用分部积分公式，得到： $$ \int e^t \cos t \mathrm{d}t = e^t \cos t - \int e^t (-\sin t) \mathrm{d}t = e^t \cos t + \int e^t \sin t \mathrm{d}t $$
将结果代入之前的积分表达式，得到： $$ \int \sin t \cdot e^t \mathrm{d}t = e^t \sin t - (e^t \cos t + \int e^t \sin t \mathrm{d}t) $$
设 $I = \int e^t \sin t \mathrm{d}t$，则有： $$ I = e^t \sin t - e^t \cos t - I $$
解这个方程，得到： $$ 2I = e^t \sin t - e^t \cos t \implies I = \frac{1}{2} (e^t \sin t - e^t \cos t) + C $$
最后要把换元的部分代回原式，你能完成剩余的部分吗?

第5步

将 $t = \ln x$ 代回，得到： $$ I = \frac{1}{2} (e^{\ln x} \sin (\ln x) - e^{\ln x} \cos (\ln x)) + C = \frac{1}{2} x [\sin (\ln x) - \cos (\ln x)] + C $$
因此，原积分的解为： $$ \int \sin (\ln x) \mathrm{d}x = \frac{1}{2} x [\sin (\ln x) - \cos (\ln x)] + C $$

4.5 $\int \frac{1}{x^2} \sqrt{\frac{1 - x}{1 + x}} \mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数，含有根号，因此考虑使用换元法来消除根号。
由于被积函数中没有明显的不同类型函数相乘，排除分部法。
初步判断，此题属于换元法。
你觉得应该如何选择换元，来消除根号呢?

第2步

观察根号内的表达式 $\sqrt{\frac{1-x}{1+x}}$，可以考虑令 $t = \sqrt{\frac{1-x}{1+x}}$。
这样，$t^2 = \frac{1-x}{1+x}$。
解这个方程得到 $x = \frac{1-t^2}{1+t^2}$。
接下来应该如何求 $\mathrm{d}x$ 呢?

第3步

由 $x = \frac{1-t^2}{1+t^2}$，求导得到 $\mathrm{d}x$： $$ \mathrm{d}x = \frac{d}{dt} \left( \frac{1-t^2}{1+t^2} \right) \mathrm{d}t = \frac{-2t(1+t^2) - 2t(1-t^2)}{(1+t^2)^2} \mathrm{d}t = -\frac{4t}{(1+t^2)^2} \mathrm{d}t $$
将换元代入原式并作化简，得 $$ \int \frac{1}{x^2} \sqrt{\frac{1-x}{1+x}} \mathrm{d}x = \int \frac{1}{\left( \frac{1-t^2}{1+t^2} \right)^2} t \cdot -\frac{4t}{(1+t^2)^2} \mathrm{d}t $$
进一步化简，得 $$ = -\int \frac{4t^2}{(1-t^2)^2} \mathrm{d}t $$
剩下的积分应该如何计算呢?

第4步

观察到 $-2 \int \frac{t \mathrm{d}(t^2)}{(1-t^2)^2}$，可以使用裂项,但也可以使用分部积分法： $$ = -2 \int t \mathrm{d}\left(\frac{1}{1-t^2}\right) $$
使用分部积分公式 $\int u \mathrm{d}v = uv - \int v \mathrm{d}u$，令 $u = t$，$\mathrm{d}v = \mathrm{d}\left(\frac{1}{1-t^2}\right)$，得 $$ = -\frac{2t}{1-t^2} + 2 \int \frac{1}{1-t^2} \mathrm{d}t $$
其中 $\int \frac{1}{1-t^2} \mathrm{d}t$ 可以拆分为 $\int \frac{1}{(1-t)(1+t)} \mathrm{d}t$，使用部分分式分解： $$ = \frac{1}{2} \int \left( \frac{1}{1-t} + \frac{1}{1+t} \right) \mathrm{d}t = \frac{1}{2} \ln \left| \frac{1+t}{1-t} \right| $$
因此，积分结果为 $$ = -\frac{2t}{1-t^2} + \ln \left| \frac{1+t}{1-t} \right| + C $$
最后要把换元的部分代回原式，你能完成剩余的部分吗?

第5步

换元代回原式并整理，得 $$ = -\frac{\sqrt{1-x^2}}{x} + \ln \left| \frac{\sqrt{1+x}+\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}} \right| + C $$

4.6 $\int\mathrm{e}^{2x}\left(1+\tan x\right)^2\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数 $\mathrm{e}^{2x}(1+\tan x)^2$，它包含指数函数和三角函数，属于两种不同类型函数相乘的情况
因此，初步判断此题属于分部法
根据分部法的口诀反对幂三指,依次当u使，我们应该如何选择 $u$ 和 $dv$ 呢?

第2步

根据口诀，指数函数 $\mathrm{e}^{2x}$ 属于“指”，三角函数 $\tan x$ 属于“三”
按照口诀，“指”应该作为 $dv$，而“三”应该作为 $u$
但是，考虑到 $\tan x$ 的导数 $\sec^2 x$ 会使积分变得更复杂，我们选择 $\mathrm{e}^{2x}$ 作为 $dv$，而 $(1+\tan x)^2$ 作为 $u$
现在，我们可以展开 $(1+\tan x)^2$ 并分别积分
展开后得到 $(1+\tan x)^2 = 1 + 2\tan x + \tan^2 x$
因此，原积分变为 $\int \mathrm{e}^{2x}(1 + 2\tan x + \tan^2 x) \mathrm{d}x$
这可以拆分为三个积分：$\int \mathrm{e}^{2x} \mathrm{d}x + 2\int \mathrm{e}^{2x} \tan x \mathrm{d}x + \int \mathrm{e}^{2x} \tan^2 x \mathrm{d}x$
第一个积分 $\int \mathrm{e}^{2x} \mathrm{d}x$ 是基本的指数积分，可以直接求解
第二个和第三个积分需要进一步处理，我们应该如何处理呢?

第3步

对于 $\int \mathrm{e}^{2x} \tan^2 x \mathrm{d}x$，我们可以使用分部积分法
令 $u = \mathrm{e}^{2x}$，$dv = \tan^2 x \mathrm{d}x$
计算 $du = 2\mathrm{e}^{2x} \mathrm{d}x$，$v = \tan x - x$（因为 $\int \tan^2 x \mathrm{d}x = \tan x - x + C$）
使用分部积分公式 $\int udv = uv - \int vdu$，我们得到 $$ \int \mathrm{e}^{2x} \tan^2 x \mathrm{d}x = \mathrm{e}^{2x} (\tan x - x) - \int (\tan x - x) 2\mathrm{e}^{2x} \mathrm{d}x $$
对于 $\int \mathrm{e}^{2x} \tan x \mathrm{d}x$，我们可以使用类似的方法
令 $u = \mathrm{e}^{2x}$，$dv = \tan x \mathrm{d}x$
计算 $du = 2\mathrm{e}^{2x} \mathrm{d}x$，$v = -\ln |\cos x|$（因为 $\int \tan x \mathrm{d}x = -\ln |\cos x| + C$）
使用分部积分公式，我们得到 $$ \int \mathrm{e}^{2x} \tan x \mathrm{d}x = \mathrm{e}^{2x} (-\ln |\cos x|) - \int (-\ln |\cos x|) 2\mathrm{e}^{2x} \mathrm{d}x $$
现在，我们可以将所有部分合并，你能完成剩余的部分吗?

第4步

合并所有部分，我们得到 $$ \int \mathrm{e}^{2x}(1+\tan x)^2 \mathrm{d}x = \mathrm{e}^{2x} + \mathrm{e}^{2x} \tan x - 2\mathrm{e}^{2x} \ln |\cos x| + \mathrm{e}^{2x} (\tan x - x) + C $$
简化后，我们得到 $$ \int \mathrm{e}^{2x}(1+\tan x)^2 \mathrm{d}x = \mathrm{e}^{2x} \tan x + C $$

5.求积分

5.1 $\int_{-\frac{n}{4}}^{\frac{n}{4}}\left(x^{2}\ln\frac{1+x}{1-x}-\cos x\right)\mathrm{d}x$

第1步: 观察积分区间和对称性

首先注意到积分区间是关于原点对称的，即 $[-\frac{n}{4}, \frac{n}{4}]$
对于在对称区间上的积分，我们通常考查被积函数的奇偶性
被积函数是 $x^2 \ln \frac{1+x}{1-x} - \cos x$，我们需要分别考查 $x^2 \ln \frac{1+x}{1-x}$ 和 $\cos x$ 的奇偶性
你觉得 $x^2 \ln \frac{1+x}{1-x}$ 和 $\cos x$ 分别是奇函数还是偶函数？

第2步: 分析被积函数的奇偶性

首先分析 $\ln \frac{1+x}{1-x}$
$\ln \frac{1+x}{1-x} = \ln (1+x) - \ln (1-x)$
由于 $\ln (1+x)$ 和 $\ln (1-x)$ 分别是奇函数和偶函数，所以 $\ln \frac{1+x}{1-x}$ 是奇函数
因此，$x^2 \ln \frac{1+x}{1-x}$ 是奇函数，因为 $x^2$ 是偶函数，乘以奇函数仍然是奇函数
$\cos x$ 是偶函数
现在你知道了 $x^2 \ln \frac{1+x}{1-x}$ 是奇函数，$\cos x$ 是偶函数，接下来应该如何利用这些信息？

第3步: 利用奇偶性简化积分

对于奇函数在对称区间上的积分，结果为0
因此，$\int_{-\frac{n}{4}}^{\frac{n}{4}} x^2 \ln \frac{1+x}{1-x} \mathrm{d}x = 0$
对于偶函数在对称区间上的积分，可以简化为两倍的正半轴上的积分
因此，$\int_{-\frac{n}{4}}^{\frac{n}{4}} \cos x \mathrm{d}x = 2 \int_{0}^{\frac{n}{4}} \cos x \mathrm{d}x$
现在你需要计算 $\int_{0}^{\frac{n}{4}} \cos x \mathrm{d}x$，你能完成这个积分吗？

第4步: 计算 $\int_{0}^{\frac{n}{4}} \cos x \mathrm{d}x$

$\int_{0}^{\frac{n}{4}} \cos x \mathrm{d}x$ 是一个基本的积分
直接使用基本积分公式，$\int \cos x \mathrm{d}x = \sin x + C$
因此，$\int_{0}^{\frac{n}{4}} \cos x \mathrm{d}x = \sin \frac{n}{4} - \sin 0 = \sin \frac{n}{4}$
由于 $\sin \frac{n}{4} = \frac{\sqrt{2}}{2}$，所以 $2 \int_{0}^{\frac{n}{4}} \cos x \mathrm{d}x = 2 \cdot \frac{\sqrt{2}}{2} = \sqrt{2}$
现在你可以将结果代入原积分表达式，你能完成最后的步骤吗？

第5步: 完成积分计算

将所有部分结合起来，原积分表达式为 $$ \int_{-\frac{n}{4}}^{\frac{n}{4}}\left(x^{2}\ln\frac{1+x}{1-x}-\cos x\right)\mathrm{d}x = 0 - \sqrt{2} = -\sqrt{2} $$
因此，最终答案是 $-\sqrt{2}$

5.2 $\int_{-1}^{1}\left(2+\sin x\right)\sqrt{1-x^{2}}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数的形式，发现它包含一个多项式函数和一个三角函数，以及一个无理式。
由于被积函数中含有两种不同类型的函数相乘，初步判断可能需要使用分部法。
但是，考虑到积分的上下限是对称的（从-1到1），我们可以先检查被积函数的奇偶性，这可能会简化问题。
你觉得应该如何检查被积函数的奇偶性呢?

第2步

被积函数可以分解为两部分：$2\sqrt{1-x^2}$ 和 $\sin x \sqrt{1-x^2}$。
检查每一部分的奇偶性：
- $2\sqrt{1-x^2}$ 是偶函数，因为 $\sqrt{1-x^2}$ 是偶函数，乘以常数2仍然是偶函数。
- $\sin x \sqrt{1-x^2}$ 是奇函数，因为 $\sin x$ 是奇函数，$\sqrt{1-x^2}$ 是偶函数，奇函数乘以偶函数仍然是奇函数。
因此，被积函数 $\left(2+\sin x\right)\sqrt{1-x^2}$ 可以看作是一个偶函数加上一个奇函数。
在对称区间上积分时，奇函数的积分为0，偶函数的积分可以通过对称性简化。
接下来应该如何利用这些性质来简化积分呢?

第3步

由于 $\sin x \sqrt{1-x^2}$ 是奇函数，在对称区间 $[-1, 1]$ 上的积分为0。
因此，原积分可以简化为只计算偶函数的积分： $$ \int_{-1}^{1}\left(2+\sin x\right)\sqrt{1-x^{2}}\mathrm{d}x = \int_{-1}^{1}2\sqrt{1-x^2}\mathrm{d}x + \int_{-1}^{1}\sin x \sqrt{1-x^2}\mathrm{d}x = \int_{-1}^{1}2\sqrt{1-x^2}\mathrm{d}x $$
由于 $2\sqrt{1-x^2}$ 是偶函数，我们可以将积分区间从 $[-1, 1]$ 缩减到 $[0, 1]$，并乘以2： $$ \int_{-1}^{1}2\sqrt{1-x^2}\mathrm{d}x = 2 \int_{0}^{1}2\sqrt{1-x^2}\mathrm{d}x = 4 \int_{0}^{1}\sqrt{1-x^2}\mathrm{d}x $$
现在需要计算 $\int_{0}^{1}\sqrt{1-x^2}\mathrm{d}x$，这个积分是一个常见的基本积分，你知道它的值吗?

第4步

$\int_{0}^{1}\sqrt{1-x^2}\mathrm{d}x$ 是一个常见的基本积分，表示单位圆在第一象限的面积的四分之一。
因此，$\int_{0}^{1}\sqrt{1-x^2}\mathrm{d}x = \frac{\pi}{4}$。
代入之前的积分结果： $$ 4 \int_{0}^{1}\sqrt{1-x^2}\mathrm{d}x = 4 \cdot \frac{\pi}{4} = \pi $$
最终答案是 $\pi$。

5.3 $\int_{-2}^{2}\left(x+\mid x\mid\right)\mathrm{e}^{-\mid x\mid}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数 $\left(x+\mid x\mid\right)\mathrm{e}^{-\mid x\mid}$，它包含两种类型的函数：线性函数和指数函数。
由于被积函数中含有绝对值符号，我们需要考虑分段函数的情况。
因此，初步判断，此题属于恒等变形+分部法。
你觉得应该如何处理绝对值符号，来简化积分呢?

第2步

由于积分区间 $[-2, 2]$ 是对称的，我们可以利用被积函数的奇偶性来简化积分。
观察 $\left(x+\mid x\mid\right)$ 和 $\mathrm{e}^{-\mid x\mid}$ 的奇偶性：
- $x$ 是奇函数，$\mid x\mid$ 是偶函数，因此 $x+\mid x\mid$ 是偶函数。
- $\mathrm{e}^{-\mid x\mid}$ 是偶函数。
因此，$\left(x+\mid x\mid\right)\mathrm{e}^{-\mid x\mid}$ 是偶函数。
对于偶函数在对称区间上的积分，可以简化为两倍在正半轴上的积分，即 $$ \int_{-2}^{2}\left(x+\mid x\mid\right)\mathrm{e}^{-\mid x\mid}\mathrm{d}x = 2 \int_{0}^{2}\left(x+\mid x\mid\right)\mathrm{e}^{-\mid x\mid}\mathrm{d}x $$
接下来应该如何处理 $\left(x+\mid x\mid\right)$ 呢?

第3步

在区间 $[0, 2]$ 上，$\mid x\mid = x$，因此 $\left(x+\mid x\mid\right) = 2x$。
所以积分变为 $$ 2 \int_{0}^{2} 2x \mathrm{e}^{-x} \mathrm{d}x = 4 \int_{0}^{2} x \mathrm{e}^{-x} \mathrm{d}x $$
现在可以使用分部法来计算这个积分。你觉得应该如何选择 $u$ 和 $dv$ 呢?

第4步

根据分部法的口诀反对幂三指,依次当u使，我们选择 $u = x$ 和 $dv = \mathrm{e}^{-x} \mathrm{d}x$。
因此，$du = \mathrm{d}x$ 和 $v = -\mathrm{e}^{-x}$。
应用分部积分公式 $\int u dv = uv - \int v du$，我们得到 $$ 4 \int_{0}^{2} x \mathrm{e}^{-x} \mathrm{d}x = 4 \left[ -x \mathrm{e}^{-x} \bigg|{0}^{2} + \intx \right] $$}^{2} \mathrm{e}^{-x} \mathrm{d
计算边界项和积分项，得 $$ 4 \left[ -2 \mathrm{e}^{-2} + \int_{0}^{2} \mathrm{e}^{-x} \mathrm{d}x \right] $$
现在计算 $\int_{0}^{2} \mathrm{e}^{-x} \mathrm{d}x$，得 $$ \int_{0}^{2} \mathrm{e}^{-x} \mathrm{d}x = -\mathrm{e}^{-x} \bigg|_{0}^{2} = -\mathrm{e}^{-2} + 1 $$
将结果代入，得 $$ 4 \left[ -2 \mathrm{e}^{-2} + 1 - \mathrm{e}^{-2} \right] = 4 \left[ 1 - 3 \mathrm{e}^{-2} \right] = 4 - 12 \mathrm{e}^{-2} $$

第5步

最终结果为 $$ \int_{-2}^{2}\left(x+\mid x\mid\right)\mathrm{e}^{-\mid x\mid}\mathrm{d}x = 4 - 12 \mathrm{e}^{-2} $$

5.4 $\int_{-1}^{1}\frac{2x^{2}+x(\mathrm{e}^{x}+\mathrm{e}^{-x})}{1+\sqrt{1-x^{2}}}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数的形式，发现它包含多项式函数和指数函数，这可能涉及到分部法。
但是，考虑到积分区间是对称的（从-1到1），我们可以先考查被积函数的奇偶性，这通常是解决对称区间积分问题的第一步。
你觉得应该如何分析被积函数的奇偶性呢？

第2步

被积函数可以分解为两部分：$\frac{2x^2}{1+\sqrt{1-x^2}}$ 和 $\frac{x(\mathrm{e}^x+\mathrm{e}^{-x})}{1+\sqrt{1-x^2}}$。
首先分析 $\frac{2x^2}{1+\sqrt{1-x^2}}$：
- 令 $f(x) = \frac{2x^2}{1+\sqrt{1-x^2}}$，则 $f(-x) = \frac{2(-x)^2}{1+\sqrt{1-(-x)^2}} = \frac{2x^2}{1+\sqrt{1-x^2}} = f(x)$，所以 $f(x)$ 是偶函数。
再分析 $\frac{x(\mathrm{e}^x+\mathrm{e}^{-x})}{1+\sqrt{1-x^2}}$：
- 令 $g(x) = \frac{x(\mathrm{e}^x+\mathrm{e}^{-x})}{1+\sqrt{1-x^2}}$，则 $g(-x) = \frac{-x(\mathrm{e}^{-x}+\mathrm{e}^x)}{1+\sqrt{1-x^2}} = -\frac{x(\mathrm{e}^x+\mathrm{e}^{-x})}{1+\sqrt{1-x^2}} = -g(x)$，所以 $g(x)$ 是奇函数。
根据奇偶函数的性质，奇函数在对称区间上的积分为0，偶函数在对称区间上的积分等于两倍其在正半轴上的积分。
因此，原积分可以简化为： $$ \int_{-1}^1 \frac{2x^2 + x(\mathrm{e}^x + \mathrm{e}^{-x})}{1+\sqrt{1-x^2}} \mathrm{d}x = 4 \int_0^1 \frac{2x^2}{1+\sqrt{1-x^2}} \mathrm{d}x $$
你能继续简化这个积分吗？

第3步

现在我们只需要计算 $\int_0^1 \frac{2x^2}{1+\sqrt{1-x^2}} \mathrm{d}x$。
观察被积函数 $\frac{2x^2}{1+\sqrt{1-x^2}}$，可以尝试进行恒等变形： $$ \frac{2x^2}{1+\sqrt{1-x^2}} = 2x^2 \cdot \frac{1}{1+\sqrt{1-x^2}} $$
注意到 $\frac{1}{1+\sqrt{1-x^2}}$ 可以进行裂项分解： $$ \frac{1}{1+\sqrt{1-x^2}} = 1 - \sqrt{1-x^2} + \frac{\sqrt{1-x^2}}{1+\sqrt{1-x^2}} $$
但是这种分解较为复杂，我们可以直接利用积分的性质来简化计算。
注意到 $\int_0^1 \frac{2x^2}{1+\sqrt{1-x^2}} \mathrm{d}x$ 可以通过几何意义来简化： $$ \int_0^1 \frac{2x^2}{1+\sqrt{1-x^2}} \mathrm{d}x = \int_0^1 \mathrm{d}x - \int_0^1 \sqrt{1-x^2} \mathrm{d}x $$
其中 $\int_0^1 \sqrt{1-x^2} \mathrm{d}x$ 是单位圆在第一象限的面积的四分之一，即 $\frac{\pi}{4}$。
因此： $$ \int_0^1 \frac{2x^2}{1+\sqrt{1-x^2}} \mathrm{d}x = 1 - \frac{\pi}{4} $$
最后，原积分的值为： $$ 4 \int_0^1 \frac{2x^2}{1+\sqrt{1-x^2}} \mathrm{d}x = 4 \left(1 - \frac{\pi}{4}\right) = 4 - \pi $$

6.求积分

6.1 $\int_0^2(x-1)^2\sqrt{2x-x^2}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数中的根号部分 $\sqrt{2x-x^2}$，这是一个典型的含有 $\sqrt{a^2-x^2}$ 形式的表达式，适合使用三角代换。
因此，初步判断此题属于恒等变形+第二类换元法。
你觉得应该如何变形，来寻找换元的部分呢?

第2步

观察根号内的表达式 $2x-x^2$，可以重写为 $1-(x-1)^2$，这样根号内的形式变为 $\sqrt{1-(x-1)^2}$，适合进行三角代换。
令 $x-1=t$，则 $dx=dt$，积分限从 $x=0$ 到 $x=2$ 变为 $t=-1$ 到 $t=1$。
将换元代入原式，得 $$ \int_0^2(x-1)^2 \sqrt{2x-x^2} \mathrm{d}x = \int_{-1}^1 t^2 \sqrt{1-t^2} \mathrm{d}t $$
由于被积函数是偶函数，可以进一步简化为 $$ \int_{-1}^1 t^2 \sqrt{1-t^2} \mathrm{d}t = 2 \int_0^1 t^2 \sqrt{1-t^2} \mathrm{d}t $$
接下来应该如何代换呢?

第3步

令 $t=\sin u$，则 $dt=\cos u \mathrm{d}u$，积分限从 $t=0$ 到 $t=1$ 变为 $u=0$ 到 $u=\frac{\pi}{2}$。
将换元代入简化后的积分，得 $$ 2 \int_0^1 t^2 \sqrt{1-t^2} \mathrm{d}t = 2 \int_0^{\frac{\pi}{2}} \sin^2 u \sqrt{1-\sin^2 u} \cos u \mathrm{d}u $$
由于 $\sqrt{1-\sin^2 u} = \cos u$，所以积分变为 $$ 2 \int_0^{\frac{\pi}{2}} \sin^2 u \cos^2 u \mathrm{d}u $$
剩下的积分应该如何计算呢?

第4步

使用三角恒等式 $\sin^2 u \cos^2 u = \frac{1}{4} \sin^2 2u$，积分变为 $$ 2 \int_0^{\frac{\pi}{2}} \frac{1}{4} \sin^2 2u \mathrm{d}u = \frac{1}{2} \int_0^{\frac{\pi}{2}} \sin^2 2u \mathrm{d}u $$
使用 $\sin^2 2u = \frac{1-\cos 4u}{2}$，积分变为 $$ \frac{1}{2} \int_0^{\frac{\pi}{2}} \frac{1-\cos 4u}{2} \mathrm{d}u = \frac{1}{4} \int_0^{\frac{\pi}{2}} (1-\cos 4u) \mathrm{d}u $$
分别积分 $1$ 和 $\cos 4u$，得 $$ \frac{1}{4} \left( \int_0^{\frac{\pi}{2}} 1 \mathrm{d}u - \int_0^{\frac{\pi}{2}} \cos 4u \mathrm{d}u \right) = \frac{1}{4} \left( \frac{\pi}{2} - 0 \right) = \frac{\pi}{8} $$
最终答案为 $\frac{\pi}{8}$。

6.2 $\int_0^\pi(\mathrm{e}^{-\cos x}-\mathrm{e}^{\cos x})\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数 $\mathrm{e}^{-\cos x} - \mathrm{e}^{\cos x}$，它包含指数函数和对数函数，但这里并没有明显的乘积形式，因此初步排除分部法。
接下来考虑换元法，观察到积分区间 $[0, \pi]$ 是对称的，但被积函数并不对称。我们可以尝试通过换元法使得积分区间对称，从而利用奇函数的性质简化计算。
因此，初步判断此题属于换元法。
你觉得应该如何选择换元，来使得积分区间对称呢？

第2步

考虑换元 $x = \frac{\pi}{2} + t$，这样可以将积分区间 $[0, \pi]$ 变换为 $[- \frac{\pi}{2}, \frac{\pi}{2}]$，这是一个对称的区间。
计算 $dx$：$dx = dt$。
将换元代入原式，得到新的积分表达式： $$ \int_0^\pi (\mathrm{e}^{-\cos x} - \mathrm{e}^{\cos x}) \mathrm{d}x = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (\mathrm{e}^{-\cos (\frac{\pi}{2} + t)} - \mathrm{e}^{\cos (\frac{\pi}{2} + t)}) \mathrm{d}t $$
利用三角函数的性质，$\cos (\frac{\pi}{2} + t) = -\sin t$，所以积分变为： $$ \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (\mathrm{e}^{\sin t} - \mathrm{e}^{-\sin t}) \mathrm{d}t $$
接下来应该如何利用奇函数的性质呢？

第3步

观察新的被积函数 $\mathrm{e}^{\sin t} - \mathrm{e}^{-\sin t}$，它是一个奇函数，因为 $(\mathrm{e}^{\sin t} - \mathrm{e}^{-\sin t})(-t) = -(\mathrm{e}^{\sin t} - \mathrm{e}^{-\sin t})$。
奇函数在对称区间上的积分为零，即 $\int_{-a}^{a} f(x) \mathrm{d}x = 0$，其中 $f(x)$ 是奇函数。
因此，$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (\mathrm{e}^{\sin t} - \mathrm{e}^{-\sin t}) \mathrm{d}t = 0$。
最终结果为： $$ \int_0^\pi (\mathrm{e}^{-\cos x} - \mathrm{e}^{\cos x}) \mathrm{d}x = 0 $$

7.求积分

7.1 $\int_{-3}^2\min\{2,x^2\}\mathrm{d}x$

第1步: 如何处理分段函数形式的积分?

首先需要明确分段函数的定义,即在不同区间内函数的具体形式
对于 $\min\{2, x^2\}$, 需要比较 $2$ 和 $x^2$ 的大小
由于 $x^2$ 是一个抛物线, 在 $x = \pm \sqrt{2}$ 处与 $2$ 相交
因此, 分段函数的定义为: $$ \min{2, x^2} = \begin{cases} 2, & -3 \leqslant x \leqslant -\sqrt{2}, \ x^2, & -\sqrt{2} < x < \sqrt{2}, \ 2, & \sqrt{2} \leqslant x \leqslant 2. \end{cases} $$
你觉得应该如何对每个区间分别积分?

第2步

根据分段函数的定义, 将积分分成三个部分: $$ \int_{-3}^2 \min{2, x^2} \mathrm{d} x = \int_{-3}^{-\sqrt{2}} 2 \mathrm{d} x + \int_{-\sqrt{2}}^{\sqrt{2}} x^2 \mathrm{d} x + \int_{\sqrt{2}}^2 2 \mathrm{d} x $$
现在分别计算每个积分:
- 对于 $\int_{-3}^{-\sqrt{2}} 2 \mathrm{d} x$, 由于 $2$ 是常数, 可以直接计算: $$ \int_{-3}^{-\sqrt{2}} 2 \mathrm{d} x = 2 \times (-\sqrt{2} - (-3)) = 2 \times (3 - \sqrt{2}) = 6 - 2\sqrt{2} $$
- 对于 $\int_{-\sqrt{2}}^{\sqrt{2}} x^2 \mathrm{d} x$, 使用幂函数积分公式: $$ \int_{-\sqrt{2}}^{\sqrt{2}} x^2 \mathrm{d} x = \left[ \frac{x^3}{3} \right]_{-\sqrt{2}}^{\sqrt{2}} = \frac{(\sqrt{2})^3}{3} - \frac{(-\sqrt{2})^3}{3} = \frac{2\sqrt{2}}{3} - \left( -\frac{2\sqrt{2}}{3} \right) = \frac{4\sqrt{2}}{3} $$
- 对于 $\int_{\sqrt{2}}^2 2 \mathrm{d} x$, 同样由于 $2$ 是常数, 可以直接计算: $$ \int_{\sqrt{2}}^2 2 \mathrm{d} x = 2 \times (2 - \sqrt{2}) = 4 - 2\sqrt{2} $$
现在将三个部分的结果相加, 你能完成剩余的部分吗?

第3步

将三个部分的积分结果相加: $$ \int_{-3}^2 \min{2, x^2} \mathrm{d} x = (6 - 2\sqrt{2}) + \frac{4\sqrt{2}}{3} + (4 - 2\sqrt{2}) $$
合并常数项和 $\sqrt{2}$ 项: $$ 6 + 4 - 2\sqrt{2} - 2\sqrt{2} + \frac{4\sqrt{2}}{3} = 10 - 4\sqrt{2} + \frac{4\sqrt{2}}{3} $$
进一步合并 $\sqrt{2}$ 项: $$ 10 - 4\sqrt{2} + \frac{4\sqrt{2}}{3} = 10 - \frac{12\sqrt{2}}{3} + \frac{4\sqrt{2}}{3} = 10 - \frac{8\sqrt{2}}{3} $$
最终结果为: $$ \int_{-3}^2 \min{2, x^2} \mathrm{d} x = 10 - \frac{8\sqrt{2}}{3} $$

7.2 $\int_{-1}^x(1-|t|)\mathrm{d}t \quad (x\geqslant-1)$

第1步: 如何处理含有绝对值的积分?

绝对值函数 $|t|$ 在 $t=0$ 处有一个分界点，因此我们需要分情况讨论。
具体来说，当 $t \geq 0$ 时，$|t| = t$；当 $t < 0$ 时，$|t| = -t$。
因此，积分 $\int_{-1}^x(1-|t|)\mathrm{d}t$ 需要根据 $x$ 的值来分段处理。
你觉得应该如何分段处理呢?

第2步

首先，考虑 $x$ 的范围。由于 $x \geq -1$，我们需要分别讨论 $x < 0$ 和 $x \geq 0$ 的情况。
当 $-1 \leq x < 0$ 时，积分区间 $[-1, x]$ 完全在负半轴上，因此 $|t| = -t$。
当 $x \geq 0$ 时，积分区间 $[-1, x]$ 跨越了 $t=0$ 的分界点，因此需要分成两部分积分：$[-1, 0]$ 和 $[0, x]$。
你能具体写出每种情况下的积分表达式吗?

第3步

当 $-1 \leq x < 0$ 时，积分表达式为： $$ \int_{-1}^x(1-|t|)\mathrm{d}t = \int_{-1}^x(1+t)\mathrm{d}t $$
当 $x \geq 0$ 时，积分表达式为： $$ \int_{-1}^x(1-|t|)\mathrm{d}t = \int_{-1}^0(1+t)\mathrm{d}t + \int_0^x(1-t)\mathrm{d}t $$
你能分别计算这两个积分吗?

第4步

当 $-1 \leq x < 0$ 时，计算 $\int_{-1}^x(1+t)\mathrm{d}t$： $$ \int_{-1}^x(1+t)\mathrm{d}t = \left.\frac{(1+t)^2}{2}\right|_{-1}^x = \frac{(1+x)^2}{2} - \frac{(1-1)^2}{2} = \frac{(1+x)^2}{2} $$
当 $x \geq 0$ 时，计算 $\int_{-1}^0(1+t)\mathrm{d}t$ 和 $\int_0^x(1-t)\mathrm{d}t$： $$ \int_{-1}^0(1+t)\mathrm{d}t = \left.\frac{(1+t)^2}{2}\right|_{-1}^0 = \frac{(1+0)^2}{2} - \frac{(1-1)^2}{2} = \frac{1}{2} $$ $$ \int_0^x(1-t)\mathrm{d}t = \left.\frac{(1-t)^2}{2}\right|_0^x = \frac{(1-x)^2}{2} - \frac{(1-0)^2}{2} = \frac{(1-x)^2}{2} - \frac{1}{2} $$
将两部分积分结果相加： $$ \int_{-1}^x(1-|t|)\mathrm{d}t = \frac{1}{2} + \left(\frac{(1-x)^2}{2} - \frac{1}{2}\right) = \frac{(1-x)^2}{2} $$
你能总结最终结果吗?

第5步

当 $-1 \leq x < 0$ 时，积分结果为： $$ \int_{-1}^x(1-|t|)\mathrm{d}t = \frac{(1+x)^2}{2} $$
当 $x \geq 0$ 时，积分结果为： $$ \int_{-1}^x(1-|t|)\mathrm{d}t = 1 - \frac{(1-x)^2}{2} $$
因此，最终结果为： $$ \int_{-1}^x(1-|t|)\mathrm{d}t = \begin{cases} \frac{(1+x)^2}{2} & \text{当 } -1 \leq x < 0 \ 1 - \frac{(1-x)^2}{2} & \text{当 } x \geq 0 \end{cases} $$

7.3 $\int_{-1}^{1}|x-y|\mathrm{e}^{x}\mathrm{d}x \quad (|y|\leqslant 1)$

第1步: 如何处理绝对值符号?

绝对值函数 $|x-y|$ 在不同区间内的表达式不同，因此需要分段讨论
当 $x \leq y$ 时，$|x-y| = y-x$
当 $x > y$ 时，$|x-y| = x-y$
因此，积分可以分为两个部分：$\int_{-1}^1|x-y|\mathrm{e}^{x}\mathrm{d}x = \int_{-1}^y(y-x)\mathrm{e}^{x}\mathrm{d}x + \int_y^1(x-y)\mathrm{e}^{x}\mathrm{d}x$
你觉得接下来应该如何进行积分?

第2步: 分别对两个部分进行积分

对于第一个部分 $\int_{-1}^y(y-x)\mathrm{e}^{x}\mathrm{d}x$，可以使用分部积分法
设 $u = y-x$，$dv = \mathrm{e}^{x}\mathrm{d}x$，则 $du = -\mathrm{d}x$，$v = \mathrm{e}^{x}$
应用分部积分公式 $\int udv = uv - \int vdu$，得 $$ \int_{-1}^y(y-x)\mathrm{e}^{x}\mathrm{d}x = \left.(y-x)\mathrm{e}^{x}\right|{-1}^y - \intx $$}^y \mathrm{e}^{x}\mathrm{d
对于第二个部分 $\int_y^1(x-y)\mathrm{e}^{x}\mathrm{d}x$，同样使用分部积分法
设 $u = x-y$，$dv = \mathrm{e}^{x}\mathrm{d}x$，则 $du = \mathrm{d}x$，$v = \mathrm{e}^{x}$
应用分部积分公式，得 $$ \int_y^1(x-y)\mathrm{e}^{x}\mathrm{d}x = \left.(x-y)\mathrm{e}^{x}\right|_y^1 - \int_y^1 \mathrm{e}^{x}\mathrm{d}x $$
现在可以计算这两个部分的积分结果，你能完成剩余的部分吗?

第3步: 计算积分结果

计算第一个部分的积分结果： $$ \left.(y-x)\mathrm{e}^{x}\right|{-1}^y - \int) $$}^y \mathrm{e}^{x}\mathrm{d}x = (y-y)\mathrm{e}^{y} - (y+1)\mathrm{e}^{-1} - \left.(\mathrm{e}^{x})\right|_{-1}^y = -(y+1)\mathrm{e}^{-1} - (\mathrm{e}^{y} - \mathrm{e}^{-1
计算第二个部分的积分结果： $$ \left.(x-y)\mathrm{e}^{x}\right|_y^1 - \int_y^1 \mathrm{e}^{x}\mathrm{d}x = (1-y)\mathrm{e}^{1} - (y-y)\mathrm{e}^{y} - \left.(\mathrm{e}^{x})\right|_y^1 = (1-y)\mathrm{e} - (\mathrm{e} - \mathrm{e}^{y}) $$
将两个部分的结果相加，得 $$ \int_{-1}^1|x-y|\mathrm{e}^{x}\mathrm{d}x = -(y+1)\mathrm{e}^{-1} - (\mathrm{e}^{y} - \mathrm{e}^{-1}) + (1-y)\mathrm{e} - (\mathrm{e} - \mathrm{e}^{y}) $$
化简结果，得 $$ \int_{-1}^1|x-y|\mathrm{e}^{x}\mathrm{d}x = 2\mathrm{e}^{y} - (y+2)\mathrm{e}^{-1} - y\mathrm{e} $$
最终答案是 $2\mathrm{e}^{y} - (y+2)\mathrm{e}^{-1} - y\mathrm{e}$

7.4 $\int_0^{\pi}\sqrt{1-\sin x}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数 $\sqrt{1-\sin x}$，它包含一个三角函数和一个无理式，这表明可能需要使用换元法。
由于被积函数中没有明显的两种不同类型函数相乘，排除分部法。
因此，初步判断此题属于恒等变形+换元法，特别是三角代换。
你觉得应该如何进行三角变换，来简化被积函数呢?

第2步

使用三角恒等式 $\sin x = 2 \sin \frac{x}{2} \cos \frac{x}{2}$，我们可以将原积分变形为： $$ \int_0^{\pi} \sqrt{1 - 2 \sin \frac{x}{2} \cos \frac{x}{2}} \mathrm{d}x $$
进一步利用恒等式 $1 - 2 \sin \frac{x}{2} \cos \frac{x}{2} = \left(\sin \frac{x}{2} - \cos \frac{x}{2}\right)^2$，我们得到： $$ \int_0^{\pi} \sqrt{\left(\sin \frac{x}{2} - \cos \frac{x}{2}\right)^2} \mathrm{d}x = \int_0^{\pi} \left|\sin \frac{x}{2} - \cos \frac{x}{2}\right| \mathrm{d}x $$
现在需要考虑绝对值的情况，如何分段处理积分呢?

第3步

由于 $\sin \frac{x}{2} - \cos \frac{x}{2}$ 在 $[0, \pi]$ 上的符号会变化，我们需要分段积分：
在 $[0, \frac{\pi}{2}]$ 上，$\sin \frac{x}{2} \geq \cos \frac{x}{2}$，所以 $\left|\sin \frac{x}{2} - \cos \frac{x}{2}\right| = \sin \frac{x}{2} - \cos \frac{x}{2}$。
在 $[\frac{\pi}{2}, \pi]$ 上，$\sin \frac{x}{2} \leq \cos \frac{x}{2}$，所以 $\left|\sin \frac{x}{2} - \cos \frac{x}{2}\right| = \cos \frac{x}{2} - \sin \frac{x}{2}$。
因此，积分可以分为两部分： $$ \int_0^{\pi} \left|\sin \frac{x}{2} - \cos \frac{x}{2}\right| \mathrm{d}x = \int_0^{\frac{\pi}{2}} \left(\sin \frac{x}{2} - \cos \frac{x}{2}\right) \mathrm{d}x + \int_{\frac{\pi}{2}}^{\pi} \left(\cos \frac{x}{2} - \sin \frac{x}{2}\right) \mathrm{d}x $$
接下来如何计算这两个积分呢?

第4步

计算第一个积分： $$ \int_0^{\frac{\pi}{2}} \left(\sin \frac{x}{2} - \cos \frac{x}{2}\right) \mathrm{d}x = \left[ -2 \cos \frac{x}{2} - 2 \sin \frac{x}{2} \right]_0^{\frac{\pi}{2}} = -2 \cos \frac{\pi}{4} - 2 \sin \frac{\pi}{4} + 2 \cos 0 + 2 \sin 0 = -2 \sqrt{2} + 2 $$
计算第二个积分： $$ \int_{\frac{\pi}{2}}^{\pi} \left(\cos \frac{x}{2} - \sin \frac{x}{2}\right) \mathrm{d}x = \left[ 2 \sin \frac{x}{2} + 2 \cos \frac{x}{2} \right]_{\frac{\pi}{2}}^{\pi} = 2 \sin \frac{\pi}{2} + 2 \cos \frac{\pi}{2} - 2 \sin \frac{\pi}{4} - 2 \cos \frac{\pi}{4} = 2 - 2 \sqrt{2} $$
将两个结果相加，得到： $$ -2 \sqrt{2} + 2 + 2 - 2 \sqrt{2} = 4(\sqrt{2} - 1) $$

第5步

综上所述，原积分的值为： $$ \int_0^{\pi} \sqrt{1-\sin x} \mathrm{d}x = 4(\sqrt{2} - 1) $$

8.求积分

8.1 $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}(x+\sin^2x)\cos^2x\mathrm{d}x$

第1步: 利用奇偶性简化积分

首先，我们需要判断被积函数中每一项的奇偶性。
$x \cos^2 x$ 是奇函数，因为 $x$ 是奇函数，$\cos^2 x$ 是偶函数，奇函数乘以偶函数仍然是奇函数。
$\sin^2 x \cos^2 x$ 是偶函数，因为 $\sin^2 x$ 和 $\cos^2 x$ 都是偶函数，偶函数乘以偶函数仍然是偶函数。
因此，积分 $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} x \cos^2 x \mathrm{d}x$ 由于对称性为0。
接下来，我们只需要计算 $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin^2 x \cos^2 x \mathrm{d}x$。

第2步

由于 $\sin^2 x \cos^2 x$ 是偶函数，我们可以将积分区间从 $[-\frac{\pi}{2}, \frac{\pi}{2}]$ 缩减到 $[0, \frac{\pi}{2}]$ 并乘以2。
因此，$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin^2 x \cos^2 x \mathrm{d}x = 2 \int_0^{\frac{\pi}{2}} \sin^2 x \cos^2 x \mathrm{d}x$。

第3步

使用三角恒等式 $\sin^2 x = 1 - \cos^2 x$，我们可以将被积函数变换为： $$ 2 \int_0^{\frac{\pi}{2}} \sin^2 x \cos^2 x \mathrm{d}x = 2 \int_0^{\frac{\pi}{2}} \sin^2 x (1 - \sin^2 x) \mathrm{d}x $$
这可以进一步拆分为两个积分： $$ 2 \int_0^{\frac{\pi}{2}} \sin^2 x \mathrm{d}x - 2 \int_0^{\frac{\pi}{2}} \sin^4 x \mathrm{d}x $$

第4步

使用 $\sin^2 x = \frac{1 - \cos 2x}{2}$，我们可以计算第一个积分： $$ 2 \int_0^{\frac{\pi}{2}} \sin^2 x \mathrm{d}x = 2 \int_0^{\frac{\pi}{2}} \frac{1 - \cos 2x}{2} \mathrm{d}x = \int_0^{\frac{\pi}{2}} (1 - \cos 2x) \mathrm{d}x $$
这等于： $$ \left[ x - \frac{\sin 2x}{2} \right]_0^{\frac{\pi}{2}} = \frac{\pi}{2} $$
对于第二个积分，使用 $\sin^4 x = (\sin^2 x)^2 = \left(\frac{1 - \cos 2x}{2}\right)^2$，我们可以计算： $$ 2 \int_0^{\frac{\pi}{2}} \sin^4 x \mathrm{d}x = 2 \int_0^{\frac{\pi}{2}} \left(\frac{1 - \cos 2x}{2}\right)^2 \mathrm{d}x $$
这等于： $$ 2 \int_0^{\frac{\pi}{2}} \frac{1 - 2\cos 2x + \cos^2 2x}{4} \mathrm{d}x = \frac{1}{2} \int_0^{\frac{\pi}{2}} (1 - 2\cos 2x + \cos^2 2x) \mathrm{d}x $$
这等于： $$ \frac{1}{2} \left( \frac{\pi}{2} - 0 + \frac{1}{2} \int_0^{\frac{\pi}{2}} \cos^2 2x \mathrm{d}x \right) = \frac{1}{2} \left( \frac{\pi}{2} + \frac{1}{2} \cdot \frac{\pi}{2} \right) = \frac{3}{8} \pi $$

第5步

将两个积分结果合并： $$ \frac{\pi}{2} - \frac{3}{8} \pi = \frac{\pi}{8} $$
因此，最终答案是： $$ \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}(x+\sin^2x)\cos^2x\mathrm{d}x = \frac{\pi}{8} $$

8.2 $\int_0^1 x(1-x^4)^{\frac{3}{2}}\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先排除分部法,因为分部法是针对被积函数中,含有两种或以上不同类型函数相乘的题目.而这道题的被积函数中含有无理式,即 $1-x^4$ 的平方根
因此初步判断,此题属于恒等变形+第二类换元法
你觉得应该如何变形,来寻找换元的部分呢?

第2步

观察题目发现被积函数中含有 $1-x^4$ 的平方根,这属于无理式
根据第二类换元法中的三角代换,当含有 $\sqrt{1-x^2}$ 时,令 $x=sint$
但这里我们需要处理的是 $1-x^4$, 可以考虑令 $x^2=sint$, 这样 $1-x^4 = 1-(sint)^2 = cos^2t$
接下来应该如何代换呢?

第3步

令 $x^2=sint$, 则 $x=\sqrt{sint}$
计算 $dx$: $2xdx = costdt$, 所以 $dx = \frac{cost}{2x}dt = \frac{cost}{2\sqrt{sint}}dt$
将换元代入原式并作化简,得 $$ \int_0^1 x(1-x^4)^{\frac{3}{2}} dx = \int_0^{\frac{\pi}{2}} \sqrt{sint} \cdot (cos^2t)^{\frac{3}{2}} \cdot \frac{cost}{2\sqrt{sint}} dt $$
化简后得 $$ \frac{1}{2} \int_0^{\frac{\pi}{2}} cos^4t dt $$
剩下的积分应该如何计算呢?

第4步

$\int_0^{\frac{\pi}{2}} cos^4t dt$ 是一个常见的三角函数积分
使用三角函数的降幂公式 $cos^2t = \frac{1+cost}{2}$, 可以得到 $$ cos^4t = (cos^2t)^2 = \left(\frac{1+cost}{2}\right)^2 = \frac{1}{4}(1+2cost+cos^2t) $$
进一步化简 $cos^2t$ 为 $\frac{1+cost}{2}$, 得 $$ cos^4t = \frac{1}{4}(1+2cost+\frac{1+cost}{2}) = \frac{1}{4}(1+2cost+\frac{1}{2}+\frac{cost}{2}) = \frac{1}{4}(\frac{3}{2}+2cost+\frac{cost}{2}) $$
因此 $$ \int_0^{\frac{\pi}{2}} cos^4t dt = \frac{1}{4} \int_0^{\frac{\pi}{2}} (\frac{3}{2}+2cost+\frac{cost}{2}) dt $$
现在可以直接积分,得 $$ \frac{1}{4} \left( \frac{3}{2}t + 2sint + \frac{1}{2}sint \right) \Big|_0^{\frac{\pi}{2}} $$
计算结果为 $$ \frac{1}{4} \left( \frac{3}{2} \cdot \frac{\pi}{2} + 2 \cdot 1 + \frac{1}{2} \cdot 1 \right) = \frac{1}{4} \left( \frac{3\pi}{4} + 2.5 \right) = \frac{3\pi}{16} + \frac{5}{16} = \frac{3\pi}{32} $$
最后的结果是 $\frac{3\pi}{32}$

8.3 $\int_{0}^{\pi}t\sin t\mathrm{d}t$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先排除换元法,因为换元法是针对被积函数中的一部分可以进行局部积分,或者含有整体无法拆分的无理式的题目.而这道题的被积函数是$t\sin t$,不包含无理式,也不容易通过局部积分简化
因此初步判断,此题属于分部法
你觉得应该如何选择$u$和$dv$呢?

第2步

根据分部法的口诀反对幂三指,依次当u使,被积函数$t\sin t$中,变量$t$属于幂函数,$\sin t$属于三角函数
因此选择$u=t$,$dv=\sin t\mathrm{d}t$
接下来应该如何应用分部积分公式$\int udv = uv-\int vdu$呢?

第3步

计算$du$和$v$:
- $du=\mathrm{d}t$
- $v=\int \sin t\mathrm{d}t = -\cos t$
应用分部积分公式,得 $$ \int_{0}^{\pi}t\sin t\mathrm{d}t = \left.(-t \cos t)\right|0^\pi - \intt $$}^{\pi}(-\cos t)\mathrm{d
化简后得 $$ \int_{0}^{\pi}t\sin t\mathrm{d}t = \left.(-t \cos t)\right|0^\pi + \intt $$}^{\pi}\cos t\mathrm{d
现在可以直接计算两个部分,你能完成剩余的部分吗?

第4步

计算$\left.(-t \cos t)\right|_0^\pi$:
- 当$t=\pi$时,$-t \cos t = -\pi \cos \pi = \pi$
- 当$t=0$时,$-t \cos t = 0$
- 因此$\left.(-t \cos t)\right|_0^\pi = \pi - 0 = \pi$
计算$\int_{0}^{\pi}\cos t\mathrm{d}t$:
- $\int_{0}^{\pi}\cos t\mathrm{d}t = \left.\sin t\right|_0^\pi = \sin \pi - \sin 0 = 0$
因此 $$ \int_{0}^{\pi}t\sin t\mathrm{d}t = \pi + 0 = \pi $$

8.4 $\int_{0}^{1}[\sqrt{2x-x^{2}}+\sqrt{(1-x^{2})^{3}}]\mathrm{d}x$

第1步: 如何处理这个积分?

观察题目中的两个被积函数，分别是 $\sqrt{2x-x^2}$ 和 $\sqrt{(1-x^2)^3}$
这两个被积函数都含有根号，且根号内是二次形式，因此考虑使用换元法
具体来说，前一个被积函数 $\sqrt{2x-x^2}$ 可以通过第一类换元法来处理，而后一个被积函数 $\sqrt{(1-x^2)^3}$ 可以通过三角代换来处理
你觉得应该如何开始处理这两个积分呢?

第2步: 处理 $\sqrt{2x-x^2}$

首先观察 $\sqrt{2x-x^2}$，可以将其改写为 $\sqrt{1-(x-1)^2}$
这样做的目的是将根号内的表达式变成一个标准的平方形式，便于后续的换元
令 $x-1=t$，则 $dx=dt$，积分限从 $x=0$ 到 $x=1$ 变为 $t=-1$ 到 $t=0$
因此，积分变为 $\int_{-1}^0 \sqrt{1-t^2} dt$
这个积分是一个常见的积分，可以通过几何意义或直接使用已知结果来求解
你能计算这个积分吗?

第3步: 计算 $\int_{-1}^0 \sqrt{1-t^2} dt$

这个积分表示的是单位圆在 $[-1, 0]$ 区间上的面积的一部分
具体来说，$\int_{-1}^0 \sqrt{1-t^2} dt$ 表示单位圆在第一象限的四分之一面积
因此，结果是 $\frac{1}{4} \pi$
你能理解这个结果的几何意义吗?

第4步: 处理 $\sqrt{(1-x^2)^3}$

观察 $\sqrt{(1-x^2)^3}$，可以令 $x=\sin t$，则 $dx=\cos t dt$，积分限从 $x=0$ 到 $x=1$ 变为 $t=0$ 到 $t=\frac{\pi}{2}$
因此，积分变为 $\int_0^{\frac{\pi}{2}} \cos^4 t dt$
这个积分可以通过使用倍角公式和递推公式来求解
你能计算这个积分吗?

第5步: 计算 $\int_0^{\frac{\pi}{2}} \cos^4 t dt$

使用倍角公式 $\cos^2 t = \frac{1+\cos 2t}{2}$，可以得到 $\cos^4 t = \left(\frac{1+\cos 2t}{2}\right)^2$
进一步展开并积分，得到 $\int_0^{\frac{\pi}{2}} \cos^4 t dt = \frac{3}{4} \times \frac{1}{2} \times \frac{\pi}{2} = \frac{3\pi}{16}$
你能理解这个计算过程吗?

第6步: 合并结果

现在我们已经分别计算了两个积分的结果
$\int_0^1 \sqrt{2x-x^2} dx = \frac{1}{4} \pi$
$\int_0^1 \sqrt{(1-x^2)^3} dx = \frac{3\pi}{16}$
因此，原积分的结果是 $\frac{1}{4} \pi + \frac{3\pi}{16} = \frac{7\pi}{16}$

9.求积分

9.1 $\int_1^{+\infty}\frac{\mathrm{d}x}{\mathrm{e}^{x+1}+\mathrm{e}^{3-x}}$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先排除分部法,因为分部法是针对被积函数中,含有两种或以上不同类型函数相乘的题目.而这道题的被积函数是单一的指数函数,即只有一种类型的函数
再排除第二类换元法,因为它是针对整体无法拆分成几个部分的无理式.这道题不含无理式
因此初步判断,此题属于恒等变形+第一类换元法
你觉得应该如何变形,来寻找换元的部分呢?

第2步

观察题目发现被积函数中包含 $\mathrm{e}^{x+1}$ 和 $\mathrm{e}^{3-x}$
为了简化表达式,可以尝试提出一个公共因子 $\mathrm{e}^2$
因此,原式可以改写为 $\int_1^{+\infty} \frac{\mathrm{d} x}{\mathrm{e}^2\left(\mathrm{e}^{x-1}+\mathrm{e}^{1-x}\right)}$
现在可以令 $x-1=t$, 这样可以将含有 $x$ 的项集中在一起,有利于整体换元
接下来应该如何代换呢?

第3步

令 $x-1=t$, 则 $x=t+1$
所以 $\mathrm{d}x = \mathrm{d}t$
积分上下限也要相应改变,当 $x=1$ 时, $t=0$; 当 $x \to +\infty$ 时, $t \to +\infty$
将换元代入原式并作化简,得 $$ \int_1^{+\infty} \frac{\mathrm{d} x}{\mathrm{e}^2\left(\mathrm{e}^{x-1}+\mathrm{e}^{1-x}\right)} = \frac{1}{\mathrm{e}^2} \int_0^{+\infty} \frac{\mathrm{d} t}{\mathrm{e}^t+\mathrm{e}^{-t}} $$
剩下的积分应该如何计算呢?

第4步

$\int_0^{+\infty} \frac{\mathrm{d} t}{\mathrm{e}^t+\mathrm{e}^{-t}}$ 可以通过分子分母同时乘以 $\mathrm{e}^t$ 来简化
因此,原式变为 $\int_0^{+\infty} \frac{\mathrm{e}^t}{1+\mathrm{e}^{2t}} \mathrm{d}t$
这个积分是一个常见的积分,可以通过 $\arctan$ 函数来求解
具体地, $\int_0^{+\infty} \frac{\mathrm{e}^t}{1+\mathrm{e}^{2t}} \mathrm{d}t = \left. \arctan(\mathrm{e}^t) \right|_0^{+\infty}$
计算 $\arctan(\mathrm{e}^t)$ 在 $0$ 和 $+\infty$ 处的值,得 $$ \left. \arctan(\mathrm{e}^t) \right|_0^{+\infty} = \arctan(\mathrm{e}^{+\infty}) - \arctan(\mathrm{e}^0) = \frac{\pi}{2} - \frac{\pi}{4} $$
最后要把换元的部分代回原式,你能完成剩余的部分吗?

第5步

将结果代回原式并整理,得 $$ \frac{1}{\mathrm{e}^2} \left( \frac{\pi}{2} - \frac{\pi}{4} \right) = \frac{1}{\mathrm{e}^2} \cdot \frac{\pi}{4} = \frac{\pi}{4 \mathrm{e}^2} $$
因此,最终答案是 $\frac{\pi}{4 \mathrm{e}^2}$

9.2 $\int_{\frac{1}{2}}^{\frac{3}{2}}\frac{\mathrm{d}x}{\sqrt{|x-x^2|}}$

第1步: 确定积分的瑕点并分解积分区间

首先观察被积函数 $\frac{1}{\sqrt{|x-x^2|}}$，注意到 $x=1$ 是一个瑕点，因为在 $x=1$ 处，$x-x^2=0$，分母为零。
因此，需要将积分区间 $\left[\frac{1}{2}, \frac{3}{2}\right]$ 分成两个部分：$\left[\frac{1}{2}, 1\right)$ 和 $\left(1, \frac{3}{2}\right]$。
这样，原积分可以分解为两个积分： $$ \int_{\frac{1}{2}}^{\frac{3}{2}} \frac{\mathrm{d} x}{\sqrt{|x-x^2|}} = \int_{\frac{1}{2}}^1 \frac{\mathrm{d} x}{\sqrt{x-x^2}} + \int_1^{\frac{3}{2}} \frac{\mathrm{d} x}{\sqrt{x^2-x}} $$
接下来，分别处理这两个积分。

第2步: 处理第一个积分 $\int_{\frac{1}{2}}^1 \frac{\mathrm{d} x}{\sqrt{x-x^2}}$

对于 $\int_{\frac{1}{2}}^1 \frac{\mathrm{d} x}{\sqrt{x-x^2}}$，首先进行恒等变形： $$ x - x^2 = \frac{1}{4} - \left(x - \frac{1}{2}\right)^2 $$
因此，积分变为： $$ \int_{\frac{1}{2}}^1 \frac{\mathrm{d} x}{\sqrt{\frac{1}{4} - \left(x - \frac{1}{2}\right)^2}} $$
这个形式与常见的积分公式 $\int \frac{\mathrm{d} x}{\sqrt{a^2 - x^2}} = \arcsin \frac{x}{a} + C$ 相似。
令 $u = x - \frac{1}{2}$，则 $\mathrm{d}u = \mathrm{d}x$，积分变为： $$ \int_{-\frac{1}{2}}^0 \frac{\mathrm{d} u}{\sqrt{\frac{1}{4} - u^2}} = \int_{-\frac{1}{2}}^0 \frac{\mathrm{d} u}{\sqrt{\left(\frac{1}{2}\right)^2 - u^2}} $$
使用公式 $\int \frac{\mathrm{d} x}{\sqrt{a^2 - x^2}} = \arcsin \frac{x}{a} + C$，得到： $$ \left. \arcsin \left(2u\right) \right|_{-\frac{1}{2}}^0 = \arcsin 0 - \arcsin (-1) = 0 - (-\frac{\pi}{2}) = \frac{\pi}{2} $$

第3步: 处理第二个积分 $\int_1^{\frac{3}{2}} \frac{\mathrm{d} x}{\sqrt{x^2-x}}$

对于 $\int_1^{\frac{3}{2}} \frac{\mathrm{d} x}{\sqrt{x^2-x}}$，同样进行恒等变形： $$ x^2 - x = \left(x - \frac{1}{2}\right)^2 - \frac{1}{4} $$
因此，积分变为： $$ \int_1^{\frac{3}{2}} \frac{\mathrm{d} x}{\sqrt{\left(x - \frac{1}{2}\right)^2 - \frac{1}{4}}} $$
这个形式与常见的积分公式 $\int \frac{\mathrm{d} x}{\sqrt{x^2 - a^2}} = \ln \left|x + \sqrt{x^2 - a^2}\right| + C$ 相似。
令 $u = x - \frac{1}{2}$，则 $\mathrm{d}u = \mathrm{d}x$，积分变为： $$ \int_{\frac{1}{2}}^1 \frac{\mathrm{d} u}{\sqrt{u^2 - \frac{1}{4}}} $$
使用公式 $\int \frac{\mathrm{d} x}{\sqrt{x^2 - a^2}} = \ln \left|x + \sqrt{x^2 - a^2}\right| + C$，得到： $$ \left. \ln \left|u + \sqrt{u^2 - \frac{1}{4}}\right| \right|_{\frac{1}{2}}^1 = \ln \left|1 + \sqrt{1 - \frac{1}{4}}\right| - \ln \left|\frac{1}{2} + \sqrt{\left(\frac{1}{2}\right)^2 - \frac{1}{4}}\right| $$
计算得： $$ \ln (1 + \frac{\sqrt{3}}{2}) - \ln \frac{1}{2} = \ln (2 + \sqrt{3}) $$

第4步: 合并结果

将两个积分的结果合并： $$ \int_{\frac{1}{2}}^{\frac{3}{2}} \frac{\mathrm{d} x}{\sqrt{|x-x^2|}} = \frac{\pi}{2} + \ln (2 + \sqrt{3}) $$
最终答案为： $$ \frac{\pi}{2} + \ln (2 + \sqrt{3}) $$

以下为较复杂的解答题

10 计算 $I=\int_0^\pi[f(x)+f''(x)]\sin x\mathrm{d}x$

第1步: 考研数学中积分题常见的考点组合是:恒等变形+换元法和恒等变形+分部法.这道题适用哪个方法?

首先观察被积函数 $[f(x) + f''(x)]\sin x$，其中包含 $f(x)$ 和 $f''(x)$，以及 $\sin x$。
由于被积函数中含有两种不同类型函数相乘（函数 $f$ 和三角函数 $\sin x$），初步判断此题属于分部法。
你觉得应该如何拆分被积函数，来应用分部积分法呢？

第2步

将积分拆分为两个部分：$I = \int_0^\pi f(x) \sin x \mathrm{d}x + \int_0^\pi f''(x) \sin x \mathrm{d}x$。
对于 $\int_0^\pi f''(x) \sin x \mathrm{d}x$，可以使用分部积分法。
令 $u = \sin x$，$dv = f''(x) \mathrm{d}x$，则 $du = \cos x \mathrm{d}x$，$v = f'(x)$。
应用分部积分公式 $\int u dv = uv - \int v du$，得到： $$ \int_0^\pi f''(x) \sin x \mathrm{d}x = \left. f'(x) \sin x \right|_0^\pi - \int_0^\pi f'(x) \cos x \mathrm{d}x $$
计算边界项 $\left. f'(x) \sin x \right|_0^\pi = f'(\pi) \sin \pi - f'(0) \sin 0 = 0$。
因此，$\int_0^\pi f''(x) \sin x \mathrm{d}x = -\int_0^\pi f'(x) \cos x \mathrm{d}x$。
接下来应该如何处理 $-\int_0^\pi f'(x) \cos x \mathrm{d}x$ 呢？

第3步

对于 $-\int_0^\pi f'(x) \cos x \mathrm{d}x$，再次应用分部积分法。
令 $u = \cos x$，$dv = f'(x) \mathrm{d}x$，则 $du = -\sin x \mathrm{d}x$，$v = f(x)$。
应用分部积分公式 $\int u dv = uv - \int v du$，得到： $$ -\int_0^\pi f'(x) \cos x \mathrm{d}x = -\left. f(x) \cos x \right|_0^\pi + \int_0^\pi f(x) \sin x \mathrm{d}x $$
计算边界项 $\left. f(x) \cos x \right|_0^\pi = f(\pi) \cos \pi - f(0) \cos 0 = -f(\pi) - f(0)$。
因此，$-\int_0^\pi f'(x) \cos x \mathrm{d}x = -(-f(\pi) - f(0)) + \int_0^\pi f(x) \sin x \mathrm{d}x = f(\pi) + f(0) - \int_0^\pi f(x) \sin x \mathrm{d}x$。
代入已知条件 $f(0) = 2$，$f(\pi) = 1$，得到： $$ -\int_0^\pi f'(x) \cos x \mathrm{d}x = 1 + 2 - \int_0^\pi f(x) \sin x \mathrm{d}x = 3 - \int_0^\pi f(x) \sin x \mathrm{d}x $$
将结果代入原积分表达式，你能完成剩余的部分吗？

第4步

将结果代入原积分表达式： $$ I = \int_0^\pi f(x) \sin x \mathrm{d}x + 3 - \int_0^\pi f(x) \sin x \mathrm{d}x = 3 $$
因此，最终答案是 $I = 3$。

11 证明 $\int_0^a f(x)\mathrm{d}x > a f\left(\frac{a}{2}\right)$

第1步: 使用泰勒公式展开 $f(x)$

由于 $f(x)$ 在 $[0,a]$ 上具有二阶导数，且 $f''(x) > 0$，我们可以利用泰勒公式在 $x = \frac{a}{2}$ 处展开 $f(x)$。
泰勒展开式为： $$ f(x) = f\left(\frac{a}{2}\right) + f'\left(\frac{a}{2}\right)\left(x - \frac{a}{2}\right) + \frac{f''(\xi)}{2!}\left(x - \frac{a}{2}\right)^2 $$ 其中 $\xi$ 介于 $\frac{a}{2}$ 和 $x$ 之间。
由于 $f''(x) > 0$，我们可以忽略余项的下界，得到： $$ f(x) \geq f\left(\frac{a}{2}\right) + f'\left(\frac{a}{2}\right)\left(x - \frac{a}{2}\right) $$

第2步

现在我们对上述不等式进行积分： $$ \int_0^a f(x) \mathrm{d} x \geq \int_0^a \left[ f\left(\frac{a}{2}\right) + f'\left(\frac{a}{2}\right)\left(x - \frac{a}{2}\right) \right] \mathrm{d} x $$
将积分拆开： $$ \int_0^a f(x) \mathrm{d} x \geq \int_0^a f\left(\frac{a}{2}\right) \mathrm{d} x + \int_0^a f'\left(\frac{a}{2}\right)\left(x - \frac{a}{2}\right) \mathrm{d} x $$

第3步

计算第一个积分： $$ \int_0^a f\left(\frac{a}{2}\right) \mathrm{d} x = f\left(\frac{a}{2}\right) \int_0^a \mathrm{d} x = a f\left(\frac{a}{2}\right) $$
计算第二个积分： $$ \int_0^a f'\left(\frac{a}{2}\right)\left(x - \frac{a}{2}\right) \mathrm{d} x $$ 令 $u = x - \frac{a}{2}$，则 $\mathrm{d}u = \mathrm{d}x$，积分限从 $-\frac{a}{2}$ 到 $\frac{a}{2}$： $$ \int_{-\frac{a}{2}}^{\frac{a}{2}} f'\left(\frac{a}{2}\right) u \mathrm{d} u = f'\left(\frac{a}{2}\right) \int_{-\frac{a}{2}}^{\frac{a}{2}} u \mathrm{d} u = f'\left(\frac{a}{2}\right) \left[ \frac{u^2}{2} \right]_{-\frac{a}{2}}^{\frac{a}{2}} = 0 $$ 因为 $\int_{-\frac{a}{2}}^{\frac{a}{2}} u \mathrm{d} u = 0$。

第4步

因此，我们有： $$ \int_0^a f(x) \mathrm{d} x \geq a f\left(\frac{a}{2}\right) $$
由于 $f(x) > 0$，且 $f''(x) > 0$，实际积分值会大于 $a f\left(\frac{a}{2}\right)$，所以： $$ \int_0^a f(x) \mathrm{d} x > a f\left(\frac{a}{2}\right) $$ 证明完成。

12 证明 $\int_a^b x f(x)\mathrm{d}x \geq \frac{a+b}{2}\int_a^b f(x)\mathrm{d}x$

第1步: 如何利用单调性证明这个不等式?

由于 $f(x)$ 在 $[a,b]$ 上连续且单调增加, 我们可以考虑构造一个辅助函数 $F(x)$, 使得 $F(x)$ 的导数能够反映出 $f(x)$ 的单调性
令 $F(x)=\int_a^x t f(t) \mathrm{d} t-\frac{a+x}{2} \int_a^x f(t) \mathrm{d} t, a \leqslant x \leqslant b$
这样构造的 $F(x)$ 包含了我们需要比较的两个积分项, 并且可以通过求导来分析其单调性
你能计算 $F(x)$ 的导数 $F'(x)$ 吗?

第2步: 计算 $F(x)$ 的导数 $F'(x)$

根据 $F(x)$ 的定义, 我们有 $$ F(x) = \int_a^x t f(t) \mathrm{d} t - \frac{a+x}{2} \int_a^x f(t) \mathrm{d} t $$
对 $F(x)$ 求导, 利用积分的导数法则, 得到 $$ F'(x) = x f(x) - \frac{1}{2} \int_a^x f(t) \mathrm{d} t - \frac{a+x}{2} f(x) $$
进一步简化, 得到 $$ F'(x) = \frac{x-a}{2} f(x) - \frac{1}{2} \int_a^x f(t) \mathrm{d} t $$
你能利用积分中值定理进一步简化 $F'(x)$ 吗?

第3步: 利用积分中值定理简化 $F'(x)$

根据积分中值定理, 存在 $\xi \in [a, x]$, 使得 $$ \int_a^x f(t) \mathrm{d} t = f(\xi)(x-a) $$
代入 $F'(x)$ 的表达式, 得到 $$ F'(x) = \frac{x-a}{2} f(x) - \frac{1}{2} f(\xi)(x-a) $$
进一步简化, 得到 $$ F'(x) = \frac{x-a}{2} [f(x) - f(\xi)] $$
由于 $f(x)$ 单调增加, $f(x) \geq f(\xi)$, 因此 $F'(x) \geq 0$
这表明 $F(x)$ 在 $[a, b]$ 上单调增加
你能利用 $F(x)$ 的单调性来证明原不等式吗?

第4步: 利用 $F(x)$ 的单调性证明原不等式

由于 $F(x)$ 在 $[a, b]$ 上单调增加, 我们有 $F(b) \geq F(a)$
计算 $F(a)$, 得到 $$ F(a) = \int_a^a t f(t) \mathrm{d} t - \frac{a+a}{2} \int_a^a f(t) \mathrm{d} t = 0 $$
因此, $F(b) \geq 0$
即 $$ \int_a^b x f(x) \mathrm{d} x - \frac{a+b}{2} \int_a^b f(x) \mathrm{d} x \geq 0 $$
从而得到 $$ \int_a^b x f(x) \mathrm{d} x \geq \frac{a+b}{2} \int_a^b f(x) \mathrm{d} x $$
原不等式得证

13 证明 $\int_a^b x f(x)\mathrm{d}x = \frac{a+b}{2}\int_a^b f(x)\mathrm{d}x$

第1步: 如何利用对称轴对函数重新表示?

由于 $f(x)$ 在 $[a,b]$ 上连续且 $y=f(x)$ 的图形关于直线 $x=\frac{a+b}{2}$ 对称，我们可以利用积分换元法来简化问题。
设 $x = a + b - t$，则 $\mathrm{d}x = -\mathrm{d}t$。
当 $x = a$ 时，$t = b$；当 $x = b$ 时，$t = a$。
因此，积分上下限需要交换，并且积分符号前需要乘以 $-1$。
具体推导如下： $$ \int_a^b x f(x) \mathrm{d} x = \int_b^a (a + b - t) f(a + b - t) (-\mathrm{d} t) = \int_a^b (a + b - t) f(a + b - t) \mathrm{d} t. $$

第2步

由于 $f(x)$ 关于 $x=\frac{a+b}{2}$ 对称，我们有 $f(x) = f(a + b - x)$。
因此，$f(a + b - t) = f(t)$。
代入上一步的结果，我们得到： $$ \int_a^b x f(x) \mathrm{d} x = \int_a^b (a + b - t) f(t) \mathrm{d} t. $$

第3步

将上一步的积分拆分为两个部分： $$ \int_a^b (a + b - t) f(t) \mathrm{d} t = (a + b) \int_a^b f(t) \mathrm{d} t - \int_a^b t f(t) \mathrm{d} t. $$
注意到 $\int_a^b t f(t) \mathrm{d} t$ 实际上就是 $\int_a^b x f(x) \mathrm{d} x$，因为 $t$ 和 $x$ 只是积分变量的符号不同。

第4步

将 $\int_a^b x f(x) \mathrm{d} x$ 移到等式左边： $$ \int_a^b x f(x) \mathrm{d} x = (a + b) \int_a^b f(x) \mathrm{d} x - \int_a^b x f(x) \mathrm{d} x. $$
合并同类项： $$ 2 \int_a^b x f(x) \mathrm{d} x = (a + b) \int_a^b f(x) \mathrm{d} x. $$
最终得到： $$ \int_a^b x f(x) \mathrm{d} x = \frac{a + b}{2} \int_a^b f(x) \mathrm{d} x. $$

14 证明：当 $0<a<b$ 时，有 $\int_a^b x f(x)\mathrm{d}x \geq \frac{1}{2}\left[b\int_0^b f(x)\mathrm{d}x - a\int_0^a f(x)\mathrm{d}x\right]$

第1步: 如何构造辅助函数来证明这个不等式?

我们需要构造一个辅助函数 $F(x)$，使得它的导数 $F'(x)$ 能够帮助我们证明不等式
观察不等式的形式，考虑构造 $F(x)$ 为： $$ F(x) = \int_a^x t f(t) \mathrm{d} t - \frac{1}{2} \left[ x \int_0^x f(t) \mathrm{d} t - a \int_0^a f(t) \mathrm{d} t \right] $$
这样构造的目的是为了利用 $f(x)$ 的单调性来证明 $F(x)$ 的单调性
你能计算 $F(x)$ 的导数 $F'(x)$ 吗?

第2步

首先，计算 $F(x)$ 的导数 $F'(x)$： $$ F'(x) = \frac{d}{dx} \left( \int_a^x t f(t) \mathrm{d} t \right) - \frac{1}{2} \left( x \frac{d}{dx} \left( \int_0^x f(t) \mathrm{d} t \right) + \int_0^x f(t) \mathrm{d} t \right) $$
使用微积分基本定理，得到： $$ F'(x) = x f(x) - \frac{1}{2} \left( x f(x) + \int_0^x f(t) \mathrm{d} t \right) $$
简化后得到： $$ F'(x) = \frac{1}{2} x f(x) - \frac{1}{2} \int_0^x f(t) \mathrm{d} t $$
你能利用 $f(x)$ 的单调性证明 $F'(x) \geq 0$ 吗?

第3步

由于 $f(x)$ 是单调增加的函数，所以对于 $t \leq x$，有 $f(t) \leq f(x)$
因此： $$ \int_0^x f(t) \mathrm{d} t \leq \int_0^x f(x) \mathrm{d} t = x f(x) $$
代入 $F'(x)$ 的表达式，得到： $$ F'(x) \geq \frac{1}{2} x f(x) - \frac{1}{2} x f(x) = 0 $$
这表明 $F(x)$ 是单调增加的函数
你能利用 $F(x)$ 的单调性证明不等式吗?

第4步

由于 $F(x)$ 是单调增加的函数，所以 $F(b) \geq F(a)$
计算 $F(a)$： $$ F(a) = \int_a^a t f(t) \mathrm{d} t - \frac{1}{2} \left[ a \int_0^a f(t) \mathrm{d} t - a \int_0^a f(t) \mathrm{d} t \right] = 0 $$
因此 $F(b) \geq 0$，即： $$ \int_a^b x f(x) \mathrm{d} x - \frac{1}{2} \left[ b \int_0^b f(x) \mathrm{d} x - a \int_0^a f(x) \mathrm{d} x \right] \geq 0 $$
这证明了不等式成立

15 求 $f(x)=\int_0^x \frac{2t-1}{t^2-t+1}\mathrm{d}t$ 在 $[-1,1]$ 上的最大值与最小值

第1步: 如何求解 $f(x)$ 的导数 $f'(x)$?

根据微积分基本定理，$f(x)$ 的导数 $f'(x)$ 等于被积函数在 $x$ 处的值，即 $$ f'(x) = \frac{2x-1}{x^2-x+1} $$
接下来应该如何求解 $f'(x) = 0$ 的解呢?

第2步

令 $f'(x) = 0$，即 $\frac{2x-1}{x^2-x+1} = 0$
解这个方程，得到 $2x-1 = 0$，即 $x = \frac{1}{2}$
这个解是 $f(x)$ 的极值点之一，接下来应该如何分析 $f(x)$ 的单调性呢?

第3步

当 $-1 < x < \frac{1}{2}$ 时，$f'(x) < 0$，说明 $f(x)$ 在这个区间内是递减的
当 $\frac{1}{2} < x < 1$ 时，$f'(x) > 0$，说明 $f(x)$ 在这个区间内是递增的
因此，$x = \frac{1}{2}$ 是 $f(x)$ 的极小值点
接下来应该如何计算 $f(x)$ 在端点和极值点的值呢?

第4步

计算 $f(1)$，即 $$ f(1) = \int_0^1 \frac{2t-1}{t^2-t+1} \mathrm{d}t $$
这个积分可以通过观察发现，被积函数是 $t^2-t+1$ 的导数，因此 $$ f(1) = \left.\ln(t^2-t+1)\right|_0^1 = \ln(1^2-1+1) - \ln(0^2-0+1) = 0 $$
计算 $f(-1)$，即 $$ f(-1) = \int_0^{-1} \frac{2t-1}{t^2-t+1} \mathrm{d}t $$
这个积分可以通过变量替换 $t = -u$ 来计算，得到 $$ f(-1) = \left.\ln(t^2-t+1)\right|_0^{-1} = \ln((-1)^2-(-1)+1) - \ln(0^2-0+1) = \ln 3 $$
计算 $f\left(\frac{1}{2}\right)$，即 $$ f\left(\frac{1}{2}\right) = \int_0^{\frac{1}{2}} \frac{2t-1}{t^2-t+1} \mathrm{d}t $$
这个积分同样可以通过观察发现，被积函数是 $t^2-t+1$ 的导数，因此 $$ f\left(\frac{1}{2}\right) = \left.\ln(t^2-t+1)\right|_0^{\frac{1}{2}} = \ln\left(\left(\frac{1}{2}\right)^2-\frac{1}{2}+1\right) - \ln(0^2-0+1) = \ln \frac{3}{4} $$
接下来应该如何比较这些值来确定最大值和最小值呢?

第5步

比较 $f(1) = 0$，$f(-1) = \ln 3$，$f\left(\frac{1}{2}\right) = \ln \frac{3}{4}$
显然，$\ln 3 > 0 > \ln \frac{3}{4}$
因此，$f(x)$ 在 $[-1,1]$ 上的最大值为 $\ln 3$，最小值为 $\ln \frac{3}{4}$
最终答案是最大值为 $\ln 3$，最小值为 $\ln \frac{3}{4}$

16 设点 $A(a,0)(a>0)$，梯形 OABC 的面积为 $S$，曲边梯形 OABC 的面积为 $S_1$，其曲边由 $y=\frac{1}{2}+x^2$ 确定，证明：$\frac{S}{S_1} < \frac{3}{2}.$

第1步: 计算梯形 OABC 的面积 $S$

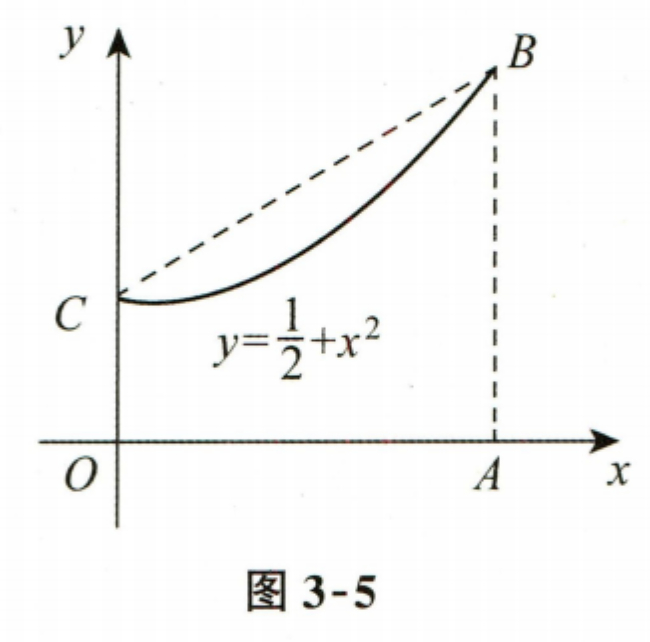
首先，我们需要确定梯形 OABC 的顶点坐标。点 $O$ 是原点 $(0,0)$，点 $A$ 是 $(a,0)$，点 $B$ 和 $C$ 在曲线 $y=\frac{1}{2}+x^2$ 上。
点 $C$ 的坐标是 $(0, \frac{1}{2})$，点 $B$ 的坐标是 $(a, a^2+\frac{1}{2})$。
梯形 OABC 的面积 $S$ 可以通过计算其顶边和底边的平均长度乘以高度来求得。
顶边 $|OC|$ 的长度是 $\frac{1}{2}$，底边 $|AB|$ 的长度是 $a^2+\frac{1}{2}$。
高度 $|OA|$ 的长度是 $a$。
因此，梯形 OABC 的面积 $S$ 为： $$ S = \frac{1}{2} \left( \frac{1}{2} + a^2 + \frac{1}{2} \right) \cdot a = \frac{1}{2} a \left( a^2 + 1 \right) $$
接下来如何计算曲边梯形 OABC 的面积 $S_1$ ?

第2步

曲边梯形 OABC 的面积 $S_1$ 可以通过积分来求得。
曲边由 $y=\frac{1}{2}+x^2$ 确定，因此我们需要计算从 $x=0$ 到 $x=a$ 的积分。
积分表达式为： $$ S_1 = \int_0^a \left( x^2 + \frac{1}{2} \right) \mathrm{d} x $$
计算这个积分： $$ S_1 = \left[ \frac{1}{3} x^3 + \frac{1}{2} x \right]_0^a = \frac{1}{3} a^3 + \frac{1}{2} a = \frac{1}{3} a \left( a^2 + \frac{3}{2} \right) $$
你能计算 $\frac{S}{S_1}$ 并证明 $\frac{S}{S_1} < \frac{3}{2}$ 吗?

第3步

现在我们有 $S = \frac{1}{2} a \left( a^2 + 1 \right)$ 和 $S_1 = \frac{1}{3} a \left( a^2 + \frac{3}{2} \right)$。
计算 $\frac{S}{S_1}$： $$ \frac{S}{S_1} = \frac{\frac{1}{2} a \left( a^2 + 1 \right)}{\frac{1}{3} a \left( a^2 + \frac{3}{2} \right)} = \frac{3}{2} \cdot \frac{a^2 + 1}{a^2 + \frac{3}{2}} $$
为了证明 $\frac{S}{S_1} < \frac{3}{2}$，我们需要证明 $\frac{a^2 + 1}{a^2 + \frac{3}{2}} < 1$。
由于 $a^2 + 1 < a^2 + \frac{3}{2}$ 对于所有 $a > 0$ 都成立，因此： $$ \frac{a^2 + 1}{a^2 + \frac{3}{2}} < 1 $$
这意味着： $$ \frac{S}{S_1} = \frac{3}{2} \cdot \frac{a^2 + 1}{a^2 + \frac{3}{2}} < \frac{3}{2} $$
因此，我们证明了 $\frac{S}{S_1} < \frac{3}{2}$。

17 设曲线 $y=\sin x (0 \leq x \leq \frac{\pi}{2})$，直线 $y=k (0 \leq k \leq 1)$ 与 $x=0$ 所围面积为 $S_1$，$y=\sin x (0 \leq x \leq \frac{\pi}{2})$，$y=k$ 与 $x=\frac{\pi}{2}$ 所围面积为 $S_2$，求 $S=S_1+S_2$ 的最小值.

第1步: 如何表示 $S_1$ 和 $S_2$ 的面积?

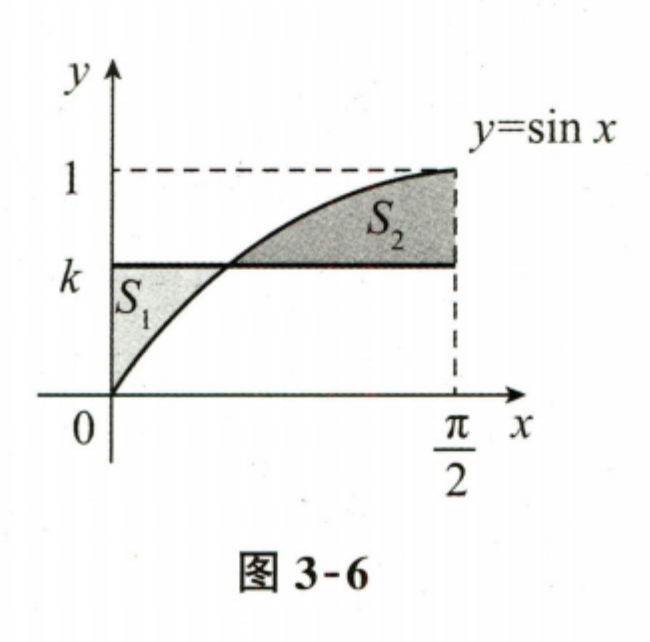
首先，我们需要用积分来表示 $S_1$ 和 $S_2$ 的面积。
$S_1$ 是由曲线 $y=\sin x$，直线 $y=k$ 和 $x=0$ 所围成的面积。
$S_2$ 是由曲线 $y=\sin x$，直线 $y=k$ 和 $x=\frac{\pi}{2}$ 所围成的面积。
设 $\sin x = k$，则 $x$ 是 $y=\sin x$ 和 $y=k$ 的交点。
因此，$S_1$ 和 $S_2$ 可以分别表示为： $$ S_1 = \int_0^x (k - \sin t) \, dt $$ $$ S_2 = \int_x^{\frac{\pi}{2}} (\sin t - k) \, dt $$
你能计算这两个积分吗？

第2步

计算 $S_1$： $$ S_1 = \int_0^x (k - \sin t) \, dt = kx - \int_0^x \sin t \, dt = kx - (-\cos x + 1) = kx + \cos x - 1 $$
计算 $S_2$： $$ S_2 = \int_x^{\frac{\pi}{2}} (\sin t - k) \, dt = \int_x^{\frac{\pi}{2}} \sin t \, dt - k \int_x^{\frac{\pi}{2}} dt = (\cos x - 1) - k \left( \frac{\pi}{2} - x \right) = \cos x + kx - \frac{1}{2} \pi k $$
现在，你能将 $k = \sin x$ 代入这两个表达式吗？

第3步

代入 $k = \sin x$： $$ S_1 = x \sin x + \cos x - 1 $$ $$ S_2 = \cos x + x \sin x - \frac{1}{2} \pi \sin x $$
因此，$S = S_1 + S_2$： $$ S = (x \sin x + \cos x - 1) + (\cos x + x \sin x - \frac{1}{2} \pi \sin x) = 2(x \sin x + \cos x) - \left(1 + \frac{\pi}{2} \sin x\right) $$
你能求 $S$ 的导数并找到其最小值吗？

第4步

求 $S$ 的导数： $$ S' = \frac{d}{dx} \left[ 2(x \sin x + \cos x) - \left(1 + \frac{\pi}{2} \sin x\right) \right] $$
使用乘积法则和链式法则： $$ S' = 2 \left( \sin x + x \cos x \right) - \frac{\pi}{2} \cos x = 2 \sin x + 2 x \cos x - \frac{\pi}{2} \cos x $$
令 $S' = 0$： $$ 2 \sin x + 2 x \cos x - \frac{\pi}{2} \cos x = 0 $$
解这个方程： $$ 2 \sin x = \frac{\pi}{2} \cos x - 2 x \cos x $$
由于 $\cos x \neq 0$，我们可以除以 $\cos x$： $$ 2 \tan x = \frac{\pi}{2} - 2 x $$
解得 $x = \frac{\pi}{4}$。
计算 $S$ 在 $x = 0$，$x = \frac{\pi}{4}$ 和 $x = \frac{\pi}{2}$ 处的值： $$ S(0) = 1, \quad S\left(\frac{\pi}{4}\right) = \sqrt{2} - 1, \quad S\left(\frac{\pi}{2}\right) = \frac{\pi}{2} - 1 $$
因此，$S$ 的最小值为 $S\left(\frac{\pi}{4}\right) = \sqrt{2} - 1$。

18 设曲线 $y=\sin x (0 \leq x \leq \frac{\pi}{2})$，$y=1$ 及 $x=0$ 所围平面图形为 $D_1$，$y=\sin x (0 \leq x \leq \pi)$ 及 $y=0$ 所围平面图形为 $D_2$。求:

$D_1$ 绕直线 $x=\frac{\pi}{2}$ 旋转一周所得体积 $V_1$。
$D_2$ 绕 $y$ 轴旋转一周所得体积 $V_2$。

第一问,第1步: 确定旋转体的体积公式

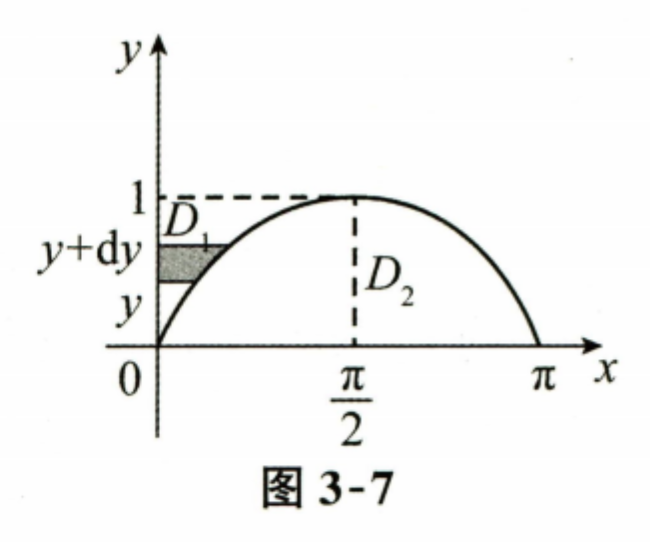
根据题目，$D_1$ 是由曲线 $y=\sin x$ 在区间 $0 \leq x \leq \frac{\pi}{2}$ 内，以及直线 $y=1$ 和 $x=0$ 所围成的区域。
我们需要计算这个区域绕直线 $x=\frac{\pi}{2}$ 旋转一周的体积。
使用微元法，考虑在 $y$ 轴上从 $y$ 到 $y+\mathrm{d}y$ 的微小区域，这个区域旋转一周形成一个环状体积。
如何计算微元体积?

第2步

任取 $[y, y+\mathrm{d}y] \subset [0, 1]$，这个微小区域旋转一周形成的体积微元为： $$ \mathrm{d} V_1 = \left[\pi\left(\frac{\pi}{2}\right)^2 - \pi\left(\frac{\pi}{2} - x\right)^2\right] \mathrm{d} y $$
其中 $x$ 是 $y=\sin x$ 的反函数，即 $x = \arcsin y$。
代入 $x = \arcsin y$，得到： $$ \mathrm{d} V_1 = \left[\pi^2 \arcsin y - \pi (\arcsin y)^2\right] \mathrm{d} y $$
你能计算积分求总体积吗?

第3步

将微元体积积分得到总体积： $$ V_1 = \int_0^1 \mathrm{d} V_1 = \pi^2 \int_0^1 \arcsin y \mathrm{d} y - \pi \int_0^1 (\arcsin y)^2 \mathrm{d} y $$
计算这两个积分： $$ \int_0^1 \arcsin y \mathrm{d} y = \left[y \arcsin y + \sqrt{1-y^2}\right]_0^1 = \frac{\pi}{2} $$ $$ \int_0^1 (\arcsin y)^2 \mathrm{d} y = \left[y (\arcsin y)^2 + 2 \sqrt{1-y^2} \arcsin y - 2 y\right]_0^1 = \frac{\pi^2}{4} - 2 $$
代入得到： $$ V_1 = \pi^2 \left(\frac{\pi}{2}\right) - \pi \left(\frac{\pi^2}{4} - 2\right) = \frac{\pi^3}{4} - \pi^2 + 2\pi $$

第2问,第1步: 确定旋转体的体积公式

$D_2$ 是由曲线 $y=\sin x$ 在区间 $0 \leq x \leq \pi$ 内，以及直线 $y=0$ 所围成的区域。
我们需要计算这个区域绕 $y$ 轴旋转一周的体积。
使用微元法，考虑在 $x$ 轴上从 $x$ 到 $x+\mathrm{d}x$ 的微小区域，这个区域旋转一周形成一个环状体积。
如何计算微元体积?

第2步

任取 $[x, x+\mathrm{d}x] \subset [0, \pi]$，这个微小区域旋转一周形成的体积微元为： $$ \mathrm{d} V_2 = 2 \pi x \cdot \sin x \mathrm{d} x $$
你能积分求总体积吗?

第3步

将微元体积积分得到总体积： $$ V_2 = \int_0^\pi 2 \pi x \sin x \mathrm{d} x $$
使用分部积分法，设 $u = x$，$dv = \sin x \mathrm{d} x$，则 $du = \mathrm{d} x$，$v = -\cos x$： $$ \int_0^\pi x \sin x \mathrm{d} x = \left[-x \cos x\right]_0^\pi + \int_0^\pi \cos x \mathrm{d} x = \pi + \left[\sin x\right]_0^\pi = \pi $$
代入得到： $$ V_2 = 2 \pi \cdot \pi = 2 \pi^2 $$

19 设星形线 $\begin{cases} x=a\cos^3 t, \\ y=a\sin^3 t \end{cases} (0 \leq t \leq 2\pi, a>0)$。求:

所围面积 $A$。
弧长 $L$。
绕 $x$ 轴旋转一周所得体积 $V$ 和表面积 $S$。

第1问: 如何利用参数方程求面积?

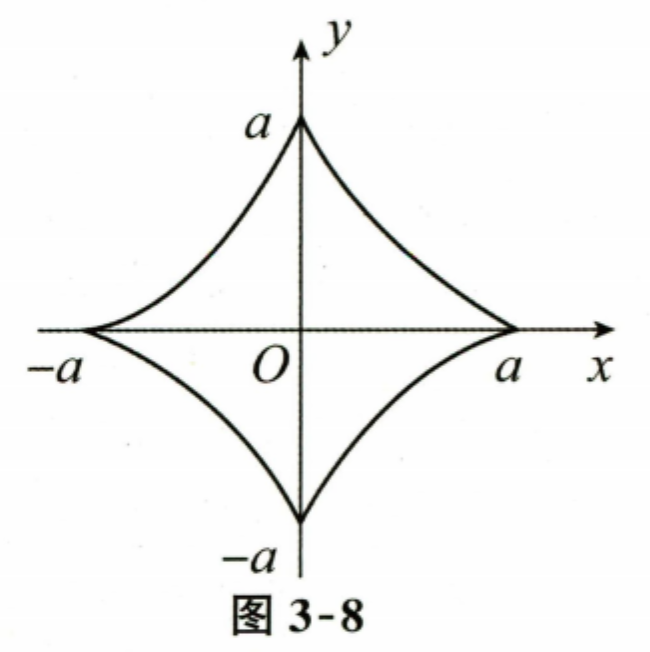
星形线的参数方程为 $x=a\cos^3 t$ 和 $y=a\sin^3 t$。
面积公式为 $A = \int_0^a y \, dx$。
由于星形线关于 $x$ 轴和 $y$ 轴对称，我们可以只计算第一象限的面积，然后乘以 4。
在第一象限，$t$ 从 $\frac{\pi}{2}$ 到 0。
计算 $dx$：$dx = \frac{d}{dt}(a\cos^3 t) \, dt = -3a\cos^2 t \sin t \, dt$。
代入面积公式：$A = 4 \int_{\frac{\pi}{2}}^0 a \sin^3 t \cdot (-3a \cos^2 t \sin t) \, dt$。
简化积分：$A = 12a^2 \int_0^{\frac{\pi}{2}} (\sin^4 t - \sin^6 t) \, dt$。
使用对称性和已知积分结果：$\int_0^{\frac{\pi}{2}} \sin^4 t \, dt = \frac{3\pi}{16}$ 和 $\int_0^{\frac{\pi}{2}} \sin^6 t \, dt = \frac{5\pi}{32}$。
最终结果：$A = 12a^2 \left( \frac{3\pi}{16} - \frac{5\pi}{32} \right) = \frac{3\pi a^2}{8}$。

第2问: 如何利用参数方程求弧长?

弧长公式为 $L = \int_0^{2\pi} \sqrt{x'(t)^2 + y'(t)^2} \, dt$。
计算 $x'(t)$ 和 $y'(t)$：$x'(t) = -3a\cos^2 t \sin t$，$y'(t) = 3a\sin^2 t \cos t$。
代入弧长公式：$L = \int_0^{2\pi} \sqrt{(-3a\cos^2 t \sin t)^2 + (3a\sin^2 t \cos t)^2} \, dt$。
简化：$L = 3a \int_0^{2\pi} \sin t \cos t \, dt$。
使用对称性和已知积分结果：$\int_0^{2\pi} \sin t \cos t \, dt = 0$，但由于对称性，实际积分范围为 $0$ 到 $\frac{\pi}{2}$，乘以 4。
最终结果：$L = 4 \cdot 3a \int_0^{\frac{\pi}{2}} \sin t \cos t \, dt = 6a$。

第3问,第1步: 如何利用参数方程求体积?

体积公式为 $V = \int_0^a \pi y^2 \, dx$。
代入参数方程：$V = 2 \int_0^a \pi (a\sin^3 t)^2 \cdot (-3a \cos^2 t \sin t) \, dt$。
简化积分：$V = 6\pi a^3 \int_0^{\frac{\pi}{2}} \sin^7 t \cos^2 t \, dt$。
使用对称性和已知积分结果：$\int_0^{\frac{\pi}{2}} \sin^7 t \cos^2 t \, dt = \frac{16}{105}$。
最终结果：$V = 6\pi a^3 \cdot \frac{16}{105} = \frac{32}{105} \pi a^3$。

第2步: 如何利用参数方程求表面积?

表面积公式为 $S = \int_0^{2\pi} 2\pi y \sqrt{x'(t)^2 + y'(t)^2} \, dt$。
代入参数方程：$S = 2 \int_0^{\frac{\pi}{2}} 2\pi a \sin^3 t \cdot 3a \sin t \cos t \, dt$。
简化积分：$S = 12\pi a^2 \int_0^{\frac{\pi}{2}} \sin^4 t \cos t \, dt$。
使用对称性和已知积分结果：$\int_0^{\frac{\pi}{2}} \sin^4 t \cos t \, dt = \frac{1}{5}$。
最终结果：$S = 12\pi a^2 \cdot \frac{1}{5} = \frac{12}{5} \pi a^2$。

20 设立体图形的底是介于 $y=x^2-1$ 和 $y=0$ 之间的平面区域，而它的垂直于 $x$ 轴的任一截面是等边三角形，求立体体积 $V$。

第1步: 确定立体图形的底面积和截面形状

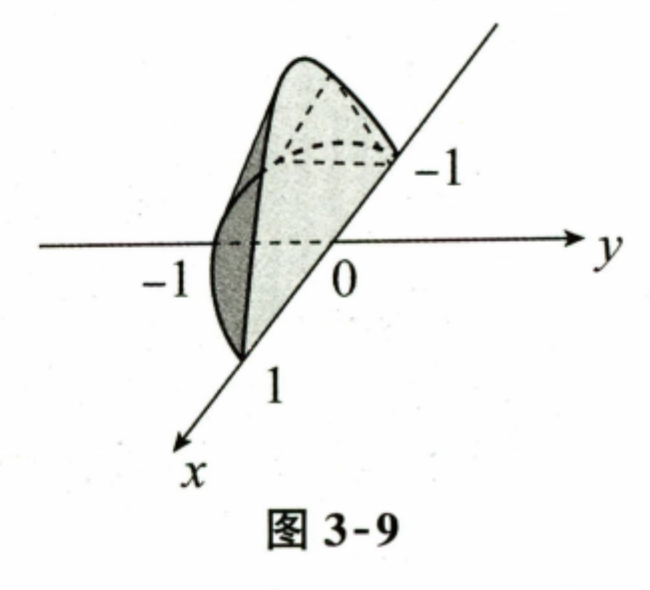
首先，我们需要明确立体图形的底面积是由 $y=x^2-1$ 和 $y=0$ 之间的区域构成的。
其次，题目明确指出垂直于 $x$ 轴的任一截面是等边三角形。
因此，我们需要计算这些等边三角形的面积，并将其作为 $x$ 的函数。
你觉得如何计算等边三角形的面积？

第2步

等边三角形的边长取决于 $y=x^2-1$ 和 $y=0$ 之间的距离，即 $x^2-1$。
等边三角形的面积公式为 $A = \frac{\sqrt{3}}{4} s^2$，其中 $s$ 是边长。
因此，截面面积 $A(x)$ 可以表示为： $$ A(x) = \frac{\sqrt{3}}{4} \left(x^2-1\right)^2 $$
接下来，我们需要将这个面积函数代入体积公式中。

第3步

立体的体积 $V$ 可以通过积分截面面积 $A(x)$ 来求得： $$ V = \int_{-1}^1 A(x) \mathrm{d} x = \frac{\sqrt{3}}{4} \int_{-1}^1 \left(x^2-1\right)^2 \mathrm{d} x $$
由于 $x^2-1$ 是偶函数，积分可以简化为： $$ V = \frac{\sqrt{3}}{2} \int_0^1 \left(x^2-1\right)^2 \mathrm{d} x $$
现在，我们需要计算这个积分。

第4步

计算 $\int_0^1 \left(x^2-1\right)^2 \mathrm{d} x$： $$ \left(x^2-1\right)^2 = x^4 - 2x^2 + 1 $$
因此，积分变为： $$ \int_0^1 \left(x^4 - 2x^2 + 1\right) \mathrm{d} x $$
分别计算每一项的积分： $$ \int_0^1 x^4 \mathrm{d} x = \left.\frac{x^5}{5}\right|_0^1 = \frac{1}{5} $$ $$ \int_0^1 -2x^2 \mathrm{d} x = -2 \left.\frac{x^3}{3}\right|_0^1 = -\frac{2}{3} $$ $$ \int_0^1 1 \mathrm{d} x = \left.x\right|_0^1 = 1 $$
将这些结果相加： $$ \int_0^1 \left(x^4 - 2x^2 + 1\right) \mathrm{d} x = \frac{1}{5} - \frac{2}{3} + 1 $$
计算结果： $$ \frac{1}{5} - \frac{2}{3} + 1 = \frac{3}{15} - \frac{10}{15} + \frac{15}{15} = \frac{8}{15} $$
你能计算最终体积吗?

第5步

将积分结果代入体积公式： $$ V = \frac{\sqrt{3}}{2} \cdot \frac{8}{15} = \frac{4\sqrt{3}}{15} $$
因此，立体的体积 $V$ 为： $$ V = \frac{4\sqrt{3}}{15} $$

21 求曲线 $x=\frac{1}{4}y^2-\frac{1}{2}\mathrm{ln~}y$ 在 $y\in\begin{bmatrix}1,\mathrm{e}\end{bmatrix}$上的弧长s

第1步: 确定弧长的计算公式

弧长的计算公式为 $s = \int_{a}^{b} \sqrt{1 + \left(\frac{dx}{dy}\right)^2} \, dy$
其中，$a$ 和 $b$ 是 $y$ 的上下限，即 $1$ 和 $\mathrm{e}$
首先需要计算 $\frac{dx}{dy}$,你能计算吗?

第2步

给定曲线方程 $x = \frac{1}{4}y^2 - \frac{1}{2}\ln y$
对 $x$ 关于 $y$ 求导，得到 $\frac{dx}{dy} = \frac{1}{2}y - \frac{1}{2y}$
你能代入弧长公式吗?

第3步

将 $\frac{dx}{dy}$ 代入弧长公式，得到 $$ \mathrm{d} s = \sqrt{1 + \left(\frac{1}{2}y - \frac{1}{2y}\right)^2} \, dy $$
计算 $\left(\frac{1}{2}y - \frac{1}{2y}\right)^2$，得到 $$ \left(\frac{1}{2}y - \frac{1}{2y}\right)^2 = \frac{1}{4}y^2 - \frac{1}{2} + \frac{1}{4y^2} $$
因此，$\mathrm{d} s = \sqrt{1 + \frac{1}{4}y^2 - \frac{1}{2} + \frac{1}{4y^2}} \, dy$
进一步简化，得到 $$ \mathrm{d} s = \sqrt{\frac{1}{4}y^2 + \frac{1}{2} + \frac{1}{4y^2}} \, dy = \frac{1}{2}\left(y + \frac{1}{y}\right) \, dy $$
你能计算这个积分吗?

第4步

现在需要计算积分 $s = \int_{1}^{\mathrm{e}} \frac{1}{2}\left(y + \frac{1}{y}\right) \, dy$
这个积分可以拆分为两个部分： $$ s = \frac{1}{2} \int_{1}^{\mathrm{e}} y \, dy + \frac{1}{2} \int_{1}^{\mathrm{e}} \frac{1}{y} \, dy $$
分别计算这两个积分： $$ \int_{1}^{\mathrm{e}} y \, dy = \frac{1}{2} y^2 \bigg|_{1}^{\mathrm{e}} = \frac{1}{2} (\mathrm{e}^2 - 1) $$
\[ \int_{1}^{\mathrm{e}} \frac{1}{y} \, dy = \ln y \bigg|_{1}^{\mathrm{e}} = \ln \mathrm{e} - \ln 1 = 1 \]
将这两个结果相加，得到 $$ s = \frac{1}{2} \left( \frac{1}{2} (\mathrm{e}^2 - 1) + 1 \right) = \frac{1}{4} (\mathrm{e}^2 + 1) $$

第三章一元函数积分学及其应用

基础题

选择题

填空题

解答题

综合题

扩展题

第三章 一元函数积分学及其应用

基础题

选择题

填空题

解答题

综合题

扩展题

第三章一元函数积分学及其应用